filmov
tv
Spinor Lorentz Transformations | How to Boost a Spinor

Показать описание
In this video, we will show you how a Dirac spinor transforms under a Lorentz transformation.
Contents:
00:00 Our Goal
00:38 Determining S
01:23 Determining T
02:30 Finite Transformation
References:
[1] Peskin, Schroeder, "An Introduction to Quantum Field Theory".
If you want to help us get rid of ads on YouTube, you can support us on Patreon!
Contents:
00:00 Our Goal
00:38 Determining S
01:23 Determining T
02:30 Finite Transformation
References:
[1] Peskin, Schroeder, "An Introduction to Quantum Field Theory".
If you want to help us get rid of ads on YouTube, you can support us on Patreon!
Spinor Lorentz Transformations | How to Boost a Spinor
What is a Four-Vector? Is a Spinor a Four-Vector? | Special Relativity
Spinors for Beginners 9: Pauli Spinors vs Weyl Spinors vs Dirac Spinors
Weyl Spinors
Spinors for Beginners 20: Lorentz Group / Algebra Representation Theory
Symmetric Physics | How Do Spinors Transform?
Spinors for Beginners 1: Introduction (Overview +Table of Contents for video series)
Lorentz Boost and Reimann Sphere (Spinors and Spacetime Chapter 1)
Spinors for Beginners 22: Dirac Equation and Gamma Matrices Deep Dive (+ chirality)
Spinor representation
QFT - 19: Spinor Representation of Lorentz Transformation (Prof. Binil Aryal, IoST, TU/ 30 May 2021)
Pauli Spinors
Spinors for Beginners 10: SU(2) double covers SO(3) [ SL(2,C) double covers SO+(1,3) ]
QFT Lecture 8: Introduction to the Lorentz Transformation & Lorentz Invariance
Transformation of a vector field according to the Lorentz algebra
The Most Mysterious Object In The Universe... Spinors Explained
Chirality VS. Helicity | Spin and Lorentz Group
Spinor Fields and the Dirac Lagrangian
QFT12.3 spinor
Rapidity in Spacetime
Spinors for Beginners 17: The spin 1/2 representations of SU(2) and SL(2,C)
Hopf Fibration Under Lorentz Transformations
Lecture 14: Lorentz Covariance of the Dirac Equation
L5.2 Introduction to four-vector in the special theory of relativity
Комментарии
 0:03:07
0:03:07
 0:02:52
0:02:52
 0:46:07
0:46:07
 0:00:16
0:00:16
 0:53:40
0:53:40
 0:23:16
0:23:16
 0:18:59
0:18:59
 0:01:10
0:01:10
 0:53:58
0:53:58
 0:11:49
0:11:49
 0:46:36
0:46:36
 0:01:00
0:01:00
 0:26:33
0:26:33
 0:55:52
0:55:52
 0:21:01
0:21:01
 0:15:04
0:15:04
 0:06:21
0:06:21
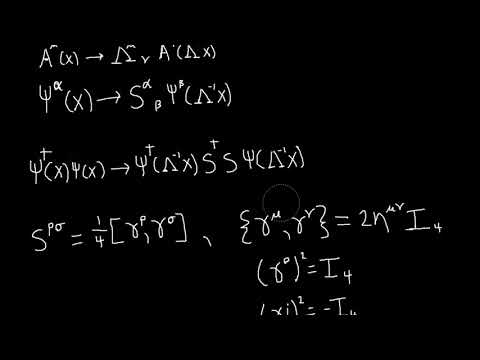 0:07:27
0:07:27
 0:05:09
0:05:09
 0:01:01
0:01:01
 0:38:19
0:38:19
 0:01:01
0:01:01
 1:18:27
1:18:27
 0:18:09
0:18:09