filmov
tv
System of first-order linear odes: repeated roots

Показать описание
Solves a system of two first-order linear odes with constant coefficients using an eigenvalue analysis. The roots of the characteristic equation are repeated.
Systems of linear first-order odes | Lecture 39 | Differential Equations for Engineers
First Order Linear Differential Equations
The Method of Integrating Factors for Linear 1st Order ODEs **full example**
Matrix Systems of Differential Equations
First Order Linear Differential Equation & Integrating Factor (introduction & example)
System of differential equations by elimination, ex1
systems of first order linear equations -- differential equations 21
8: Eigenvalue Method for Systems - Dissecting Differential Equations
How to Solve First Order Linear Differential Equations
Converting a Higher Order ODE Into a System of First Order ODEs
4 Types of ODE's: How to Identify and Solve Them
First order, Ordinary Differential Equations.
System of First Order Differential Equations || Matrix Method || RSC || Dr. Abhishek
Linear Differential Equations & the Method of Integrating Factors
Differential equations, a tourist's guide | DE1
Differential equation introduction | First order differential equations | Khan Academy
Solving First order linear differential equation
(3.1.3) Changing Higher Order ODEs and Systems of ODEs as First Order Systems
Autonomous Equations, Equilibrium Solutions, and Stability
System of first-order linear odes: complex roots
Convert Second-order ODE to First-order Linear System
ODE | Linear versus nonlinear
Writing a second order differential equation as a system of first order equations.
Coupled System of Differential Equations
Комментарии
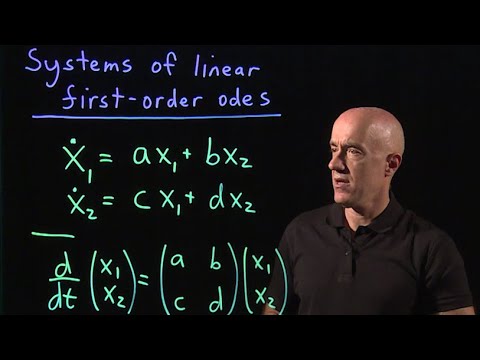 0:08:28
0:08:28
 0:22:28
0:22:28
 0:05:07
0:05:07
 0:24:58
0:24:58
 0:20:34
0:20:34
 0:20:44
0:20:44
 0:34:02
0:34:02
 0:08:57
0:08:57
 0:10:53
0:10:53
 0:13:30
0:13:30
 0:06:57
0:06:57
 0:48:35
0:48:35
 0:18:24
0:18:24
 0:11:36
0:11:36
 0:27:16
0:27:16
 0:07:49
0:07:49
 0:11:52
0:11:52
 0:07:56
0:07:56
 0:10:20
0:10:20
 0:14:44
0:14:44
 0:03:51
0:03:51
 0:03:26
0:03:26
 0:04:16
0:04:16
 0:07:19
0:07:19