filmov
tv
Expressing sin(x) and cos(x) in terms of t = tan(x/2)

Показать описание
In this video, I derive the following identities:
sin(x) = 2*t / (1 + t^2)
cos(x) = (1 - t^2) / (1 + t^2)
These identities are important when it comes to simplifying integrals of rational fractions involving sin(x), cos(x) and tan(x).
The process is simple, but we need to remember the double angle formulas:
sin(2a) = 2*sin(a)*cos(a)
cos(2a) = cos^2(a) - sin^2(a)
We also need to remember that in terms of tan(x):
sin(x) = tan(x) / sqrt( 1 + tan^2(x) )
cos(x) = 1 / sqrt( 1 + tan^2(x) )
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
sin(x) = 2*t / (1 + t^2)
cos(x) = (1 - t^2) / (1 + t^2)
These identities are important when it comes to simplifying integrals of rational fractions involving sin(x), cos(x) and tan(x).
The process is simple, but we need to remember the double angle formulas:
sin(2a) = 2*sin(a)*cos(a)
cos(2a) = cos^2(a) - sin^2(a)
We also need to remember that in terms of tan(x):
sin(x) = tan(x) / sqrt( 1 + tan^2(x) )
cos(x) = 1 / sqrt( 1 + tan^2(x) )
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
Animated mathematics Equation of Sin (x) and Cos (x)
Expressing sin(x) and cos(x) in terms of tan(x)
Expressing sin(x) and cos(x) in terms of t = tan(x/2)
Sine and Cosine Explained Visually! #math #trigonometry #calculus #explained
What is sin(x)sin(x) + cos(x)cos(x) = ?
Express sin 4x in terms of sin x and cos x
Differentiation - sin(x) and cos(x)
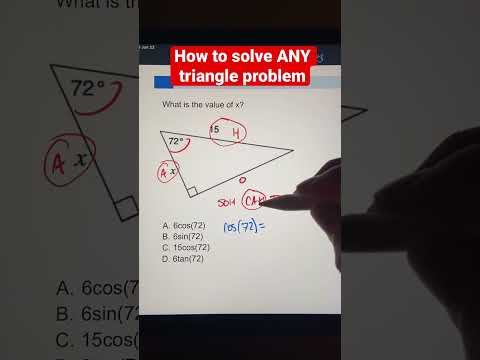
Missing Side of a Triangle Trigonometry Problem SOH CAH TOA (sin, cos, tan) #shorts #maths #math
Simplify the expression (sec x - cos x) / tan x
Express 6 sin x cos x in form a sin bx. Solve 6 sin x cos x = 3/2. [pi/4, pi/2]
sin(x) and cos(x) graph 📊 #sinx #cosx
Solve equation sqrt(3) sin x + cos x =1. Give general solution.
Half Angle Formula: Express sin(x/2) in terms of cos(x). Express cos(x/2) in terms of cos(x)
Simplifying A Nice Trigonometric Expression
weierstrass substitution, integral of 1/(1+sin(x)+cos(x))
Simplifying A Trigonometric Expression
Solve sin(x) = -0.5 without a calculator #shorts #trigonometry #unitcircle #cosine #maths #math
Trigonometric differentiation of sin(x) and cos(x) | Easy hack |
How To Use Reference Angles to Evaluate Trigonometric Functions
Derivative of sin(x) and cos(x), PROOF
cos(arcsinx) as an algebraic expression, cosine of inverse sine x
Write an algebraic expression for cos(sin^-1 x), cosine of inverse sine x
Trigonometric Graphs | Graph of Sin Cos Tan Sec Cosec Cot #physics #maths #shorts
Proving Trigonometric Expression
Комментарии
 0:00:16
0:00:16
 0:04:28
0:04:28
 0:04:53
0:04:53
 0:00:32
0:00:32
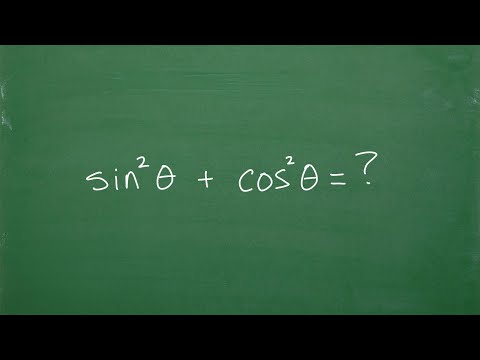 0:08:14
0:08:14
 0:04:15
0:04:15
 0:05:35
0:05:35
 0:00:39
0:00:39
 0:01:36
0:01:36
 0:03:33
0:03:33
 0:00:10
0:00:10
 0:03:59
0:03:59
 0:06:39
0:06:39
 0:00:32
0:00:32
 0:02:34
0:02:34
 0:00:59
0:00:59
 0:00:45
0:00:45
 0:00:16
0:00:16
 0:10:59
0:10:59
 0:09:18
0:09:18
 0:03:41
0:03:41
 0:03:28
0:03:28
 0:00:23
0:00:23
 0:00:58
0:00:58