filmov
tv
Expressing sin(x) and cos(x) in terms of tan(x)

Показать описание
In this video, I show how with a right angled triangle with hypotenuse 1, sides (a) and (b), and using Pythagoras' Theorem, that:
cos(x) = 1 / sqrt( 1 + tan^2(x)) and
sin(x) = tan(x) / sqrt( 1 + tan^2(x))
From the Pythagorean Identity: cos^2(x) + sin^2(x) = 1. If we divide this by cos^2x, we get...
1 + tan^2(x) = 1/cos^2(x)
And if we flip this over, we get...
cos^2(x) = 1/[1 + tan^2(x)]
And taking the square root of both sides...
cos(x) = 1/√[1 + tan^2(x)]
For sin(x), we note that sin(x)/cos(x) = tan(x), which we can rearrange to sin(x) = tan(x)cos(x). And thus...
sin(x) = tan(x)/√[1 + tan^2(x)]
These are useful trigonometric identities that can help us when performing integrals of trig functions.
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
cos(x) = 1 / sqrt( 1 + tan^2(x)) and
sin(x) = tan(x) / sqrt( 1 + tan^2(x))
From the Pythagorean Identity: cos^2(x) + sin^2(x) = 1. If we divide this by cos^2x, we get...
1 + tan^2(x) = 1/cos^2(x)
And if we flip this over, we get...
cos^2(x) = 1/[1 + tan^2(x)]
And taking the square root of both sides...
cos(x) = 1/√[1 + tan^2(x)]
For sin(x), we note that sin(x)/cos(x) = tan(x), which we can rearrange to sin(x) = tan(x)cos(x). And thus...
sin(x) = tan(x)/√[1 + tan^2(x)]
These are useful trigonometric identities that can help us when performing integrals of trig functions.
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
Animated mathematics Equation of Sin (x) and Cos (x)
Expressing sin(x) and cos(x) in terms of tan(x)
Expressing sin(x) and cos(x) in terms of t = tan(x/2)
What is sin(x)sin(x) + cos(x)cos(x) = ?
Sine and Cosine Explained Visually! #math #trigonometry #calculus #explained
Differentiation - sin(x) and cos(x)
Expressing Tan(x) in terms of Cos(x)
sin(x) and cos(x) graph 📊 #sinx #cosx
A Level Physics Paper 1 Periodic Motion Ultimate Revision Session
Simplify the expression (sec x - cos x) / tan x
Trigonometric differentiation of sin(x) and cos(x) | Easy hack |
Express 6 sin x cos x in form a sin bx. Solve 6 sin x cos x = 3/2. [pi/4, pi/2]
Simplifying A Nice Trigonometric Expression
Solve sin(x) = -0.5 without a calculator #shorts #trigonometry #unitcircle #cosine #maths #math
Simplifying A Trigonometric Expression
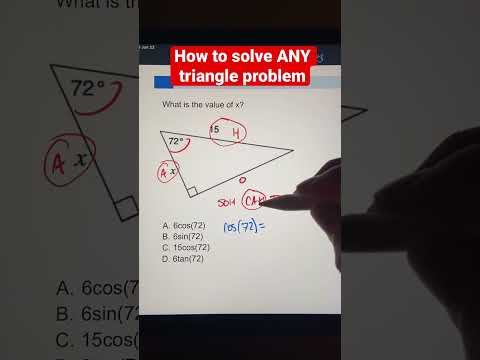
Missing Side of a Triangle Trigonometry Problem SOH CAH TOA (sin, cos, tan) #shorts #maths #math
How To Use Reference Angles to Evaluate Trigonometric Functions
Verify (sin x + cos x)^2 = 1 + 2sinxcosx
Solve equation sqrt(3) sin x + cos x =1. Give general solution.
Derivative of sin(x) and cos(x), PROOF
weierstrass substitution, integral of 1/(1+sin(x)+cos(x))
Proving Trigonometric Expression
#Trigonometry all formulas
Write an algebraic expression for cos(sin^-1 x), cosine of inverse sine x
Комментарии
 0:00:16
0:00:16
 0:04:28
0:04:28
 0:04:53
0:04:53
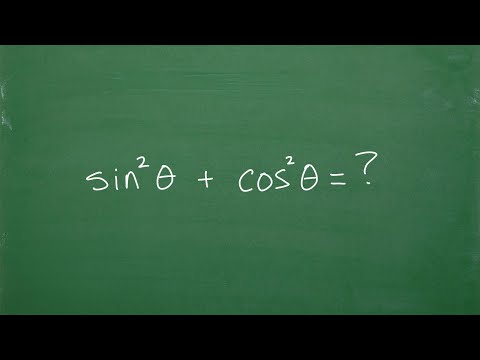 0:08:14
0:08:14
 0:00:32
0:00:32
 0:05:35
0:05:35
 0:06:13
0:06:13
 0:00:10
0:00:10
 2:56:12
2:56:12
 0:01:36
0:01:36
 0:00:16
0:00:16
 0:03:33
0:03:33
 0:00:32
0:00:32
 0:00:45
0:00:45
 0:00:59
0:00:59
 0:00:39
0:00:39
 0:10:59
0:10:59
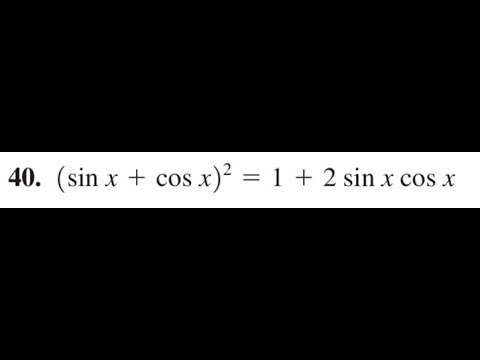 0:00:46
0:00:46
 0:03:59
0:03:59
 0:09:18
0:09:18
 0:02:34
0:02:34
 0:00:58
0:00:58
 0:00:16
0:00:16
 0:03:28
0:03:28