filmov
tv
Math Olympiad | Solve for x & y | 95% Failed to solve!

Показать описание
Also Watch our Most Viral Interesting Math Olympiad Problem:
Subscribe to our channel and press the bell icon 🔔 for daily Brainstorming Math videos →
*****************************************************************************
#exponentialproblems #matholympiad #maths #algebra
Subscribe to our channel and press the bell icon 🔔 for daily Brainstorming Math videos →
*****************************************************************************
#exponentialproblems #matholympiad #maths #algebra
Solving an IMO Problem in 6 Minutes!! | International Mathematical Olympiad 1979 Problem 1
Maths Olympiad 🔥 How to Solve Maths Olympiad Problem | Jk Campus
Norway Math Olympiad Question | You should be able to solve this!
A Nice Math Olympiad Exponential Equation 3^x = X^9
Can you solve for X? | (Segment length) | #math #maths | #geometry
Math Olympiad Question | You should know how to solve this!!
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
Solving the Legendary IMO Problem 6 in 8 minutes | International Mathematical Olympiad 1988
A Very Nice Math Olympiad Problem| Can You Solve For a and b? | Exponential equation
Math Olympiad Solution.
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!
A beautiful international math olympiad problem
Luxembourg - Math Olympiad Question | You should know this trick
UK - Math Olympiad Question | You should be able to solve this without calculators!!
Math Olympiad Question | You should know this trick!!
Math Olympiad| Nice exponential math problem| solve for x
Mathematical Olympiad | Solve for a+b | Math Olympiad Preparation
A great math olympiad question | Power rules
New Zealand - Math olympiad Question
Math Olympiad Question | Algebra Equation Solving | You should be able to solve this!!
South Africa Math Olympiad Question
This U.S. Olympiad Coach Has a Unique Approach to Math
Solving the hardest question of a British Mathematical Olympiad
France | A great math olympiad question | Can You Solve?
Комментарии
 0:06:40
0:06:40
 0:15:23
0:15:23
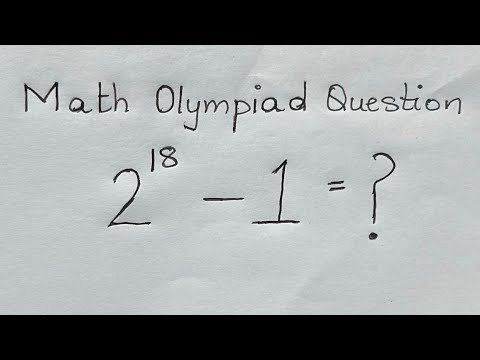 0:03:21
0:03:21
 0:02:34
0:02:34
 0:06:41
0:06:41
 0:02:24
0:02:24
 0:01:54
0:01:54
 0:08:03
0:08:03
 0:10:49
0:10:49
 0:09:33
0:09:33
 0:08:40
0:08:40
 0:01:00
0:01:00
 0:02:51
0:02:51
 0:03:20
0:03:20
 0:00:33
0:00:33
 0:02:53
0:02:53
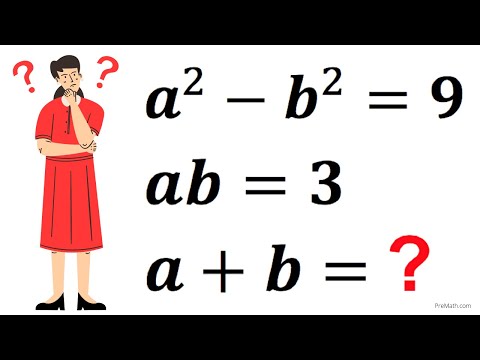 0:08:59
0:08:59
 0:10:46
0:10:46
 0:01:12
0:01:12
 0:09:15
0:09:15
 0:06:45
0:06:45
 0:03:20
0:03:20
 0:11:26
0:11:26
 0:10:31
0:10:31