filmov
tv
Real Analysis Ep 12: Subsequences & Bolzano Weierstrauss

Показать описание
Episode 12 of my videos for my undergraduate Real Analysis course at Fairfield University. This is a recording of a live class.
This episode is about subsequences and the Bolzano-Weierstrauss theorem.
This episode is about subsequences and the Bolzano-Weierstrauss theorem.
Real Analysis Ep 12: Subsequences & Bolzano Weierstrauss
Intro to Subsequences | Real Analysis
Real Analysis ep12: Monotone convergence theorem (Sep 30, 2022)
Real Analysis Chapter 4.4: Subsequences
Advanced Calculus I, Part 12, Every Sequence has a Convergent Subsequence, The Sequential Compactnes
Subsequences
Subsequence Theorem Introduction [Real Analysis]
Subsequences Introduction [Real Analysis]
Intro Real Analysis, Lec 8: Subsequences, Bolzano-Weierstrass, Cauchy Criterion, Limsup & Liminf
Real Analysis Exam 1 Review Problems and Solutions
Limit Points of a Real Sequences
What is Cauchy Sequence?? #sequence and series #real analysis #viral #cuet #iit jam
Lecture 9: Limsup, Liminf, and the Bolzano-Weierstrass Theorem
Math 441 - 3.3 Compact Sets
Find limit #convergence#sequence@The Math Bunny . shaping a bright future
Subsequence of convergent sequence is convergent and converges to same limit| PROOF
47 Subsequences of convergent sequences part 2
Lecture 12: The Ratio, Root, and Alternating Series Tests
Lec 9 || Real Analysis complete course || Subsequence Limit supremum limit infimum Cauchy sequence
Teaching myself an upper level pure math course (we almost died)
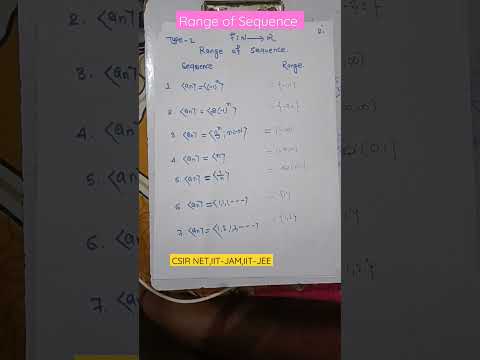
#Real analysis #Range of Sequences #CSIR NET#GATE#IIT-JAM#IUT-JEE
Properties of Continuous Functions - Real Analysis | Lecture 12
Math | Real Sequences | Subsequences | Lect.-20 | Dr. S.S.Bellale | DSCL
NIT Warangal || #nitwarangal ||#messfood || #mess || #nitwarangalmess ||#nitw ||#topnit || #nit
Комментарии
 0:33:45
0:33:45
 0:15:25
0:15:25
 0:48:36
0:48:36
 0:39:14
0:39:14
 0:24:32
0:24:32
 0:13:10
0:13:10
 0:15:29
0:15:29
 0:12:00
0:12:00
 0:57:23
0:57:23
 1:05:33
1:05:33
 1:07:11
1:07:11
 0:00:09
0:00:09
 1:13:43
1:13:43
 0:17:29
0:17:29
 0:00:59
0:00:59
 0:06:20
0:06:20
 0:05:03
0:05:03
 1:00:21
1:00:21
 0:38:43
0:38:43
 0:19:28
0:19:28
 0:01:01
0:01:01
 0:37:34
0:37:34
 0:40:09
0:40:09
 0:00:26
0:00:26