Lecture 12: The Ratio, Root, and Alternating Series Tests

preview_player
Показать описание
MIT 18.100A Real Analysis, Fall 2020
Instructor: Dr. Casey Rodriguez

We show three important tests for convergence of infinite series: the ratio, root, and alternating series tests.

License: Creative Commons BY-NC-SA

  1. MIT OpenCourseWare
  2. Ratio test
  3. alternating series test
  4. infinite series
  5. root test
Рекомендации по теме
Lecture 12: The 1:00:21

Lecture 12: The Ratio, Root, and Alternating Series Tests

Calculus II, Lecture 0:38:55

Calculus II, Lecture 17: Root, ratio, & comparison tests

IIT Bombay Lecture 0:00:12

IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit

The Hardest Math 0:00:28

The Hardest Math Test

Lecture 12: Magnetics, 0:50:55

Lecture 12: Magnetics, Part 4

Can you solve 0:00:57

Can you solve this 150 years old puzzle? #shorts

Spiraling squares | 0:03:50

Spiraling squares | Lecture 12 | Fibonacci Numbers and the Golden Ratio

The Simplest Math 0:22:09

The Simplest Math Problem No One Can Solve - Collatz Conjecture

Lecture 5 ME 1:07:24

Lecture 5 ME 6250; damping ratio, Harmonic response, Ples of a characteristic equation

Lecture 12: Cities, 0:38:51

Lecture 12: Cities, Future Fossil Fuel Use, CCUS, and Nuclear Energy

Dynamic Reduction Methods. 0:37:15

Dynamic Reduction Methods. Lecture 12, Part A.

Logarithms, Explained - 0:03:34

Logarithms, Explained - Steve Kelly

Lecture 12: The 1:23:48

Lecture 12: The Dirac Well and Scattering off the Finite Step

BIOPL3420 - Plant 1:15:39

BIOPL3420 - Plant Physiology - Lecture 12

Lecture 12: Coupled 0:32:27

Lecture 12: Coupled roots derivation continued

Trigonometry Concepts - 0:32:35

Trigonometry Concepts - Don't Memorize! Visualize!

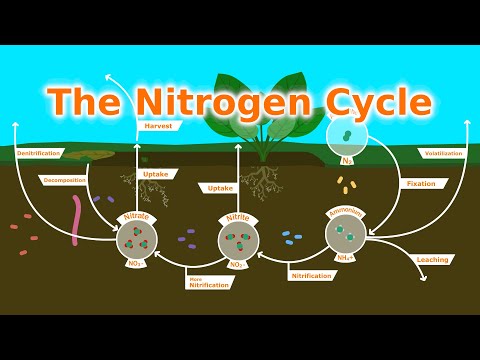
Understanding Our Soil: 0:04:30

Understanding Our Soil: The Nitrogen Cycle, Fixers, and Fertilizer

The magic of 0:06:25

The magic of Fibonacci numbers | Arthur Benjamin | TED

Ratios | All 0:05:57

Ratios | All About Ratios

The most unexpected 0:05:13

The most unexpected answer to a counting puzzle

How to Answer 0:00:27

How to Answer Any Question on a Test

The Maths Prof: 0:04:52

The Maths Prof: Standard Form (part 1)

ECAT Maths Lecture 0:06:16

ECAT Maths Lecture Series, 2nd Year Maths, lec 2,Section Ratio Formula-Ch 18

Fundamental Theorem of 0:11:30

Fundamental Theorem of Calculus Part 1

Комментарии
Автор

So, I guess this marks the end of:
Single Variable analysis: Sequences and Series.
As always, I praise MIT OCW and similar programs for this free information.

So far, it's been great. Although the proofs kinda beat me, it is reeally nice to see the proofs of the theorems you wouldn't see in your classic calculus class. (Yes, this implies that I haven't even taken Calculus formally yet.)

Since I try to understand the proofs uniquely to grasp a better understanding of usual Calculus, I've been mostly focused on applications exercises more than proofs, but trust me, I've understood mostly everything so far, in a kind of ordered way, somehting like this:

Understanding Calculus ≤ Understanding of analysis for calculus ≤ Understanding of analysis

We take the limit as Understanding goes to infinity, then :

L ≤ Understanding of analysis for Calculus ≤ U
(Asuming the others converge, by squeeze theorem)
and therefore: there exists a B≥0 s.t |Understanding(analysis, calculus)|≤B (converges <=> bounded)

*This does not make ANY sense, its just fun rambling and its probably wrong anyway.

Javy_Chand
Автор

at 34'40, limsupXn should be >1 instead of >= 1 right?

HaozheJiang