Derivatives of Reciprocal Trigonometric Functions - Grade 12 Calculus (Math Hacks)

#shorts

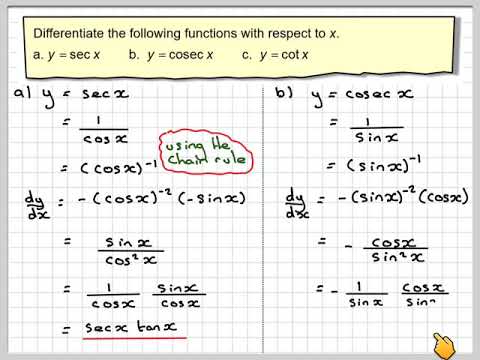
In this video, we are covering how to calculate the derivatives of reciprocal trigonometric functions. The reciprocal trigonometric functions are: 1/sin(x) = csc(x); 1/cos(x) = sec(x); and 1/tan(x) = cot(x). The formulas for calculating the derivatives of these reciprocal trigonometric functions are:

(d/dy)csc(x) = -csc(X)cot(x)

(d/dy)sec(x) = sec(x)tan(x)

(d/dy)cot(x) = [csc(x)]^2

While it is best to memorize these derivatives, we can also calculate them manually with knowledge of the chain rule and the quotient rule. Additionally, we will need to know how to calculate the derivatives of the standard trigonometric functions:

(d/dy)sin(x) = cos(x)

(d/dy)cos(x) = -sin(x)

(d/dy)tan(x) = [sec(x)]^2

For additional videos covering Grade 12 Calculus concepts, check out the playlist below:

For a reminder on how to use product rule, check out this short below:
(Video coming soon)

For a reminder on how to use quotient rule, check out this short below:
(Video coming soon)