Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)

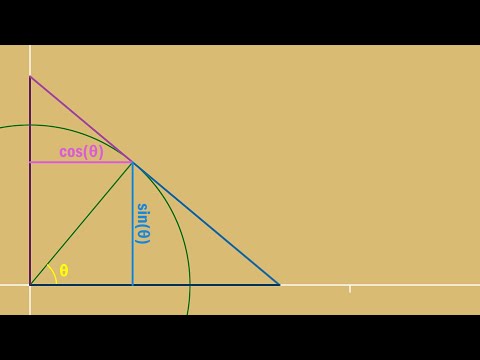
In this video, we show a single diagram consisting of various triangles that connects the six primary trig functions (sine, cosine, tangent, secant, cosecant, and cotangent) to lengths of line segments created from the unit circle (circle of radius 1). We use the diagram to explain features about why tangent and secant aren't defined at pi/2, the possible outputs of these six functions, and the Pythagorean trig identities. We also briefly discuss the fact that the "co" on three of the functions refer to the "complementary angle."

This animation is based on a classic diagram for describing the six main trig functions. If you want to know more trig identities, check out my playlist:

or check out this Wikipedia article:

Here is an interactive version from Tien Chih using Desmos:

Here are alternate videos with the same diagram:

#math​ #mathvideo #math #trigonometry #trigidentities #identity #triangle #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #circle #pythagoreantheorem #obtuseangle #acuteangle #angle #sine #cosine #tangent #secant #cosecant #cotangent #learnmaths

To learn more about animating with manim, check out:
_______________
Music in this video:

[RandyKing]

i’ve never seen this diagram…even a static version is quite informative, but the animation knocks it out the park…thanks!

[clairecelestin]

This diagram is basically a full semester of trig, and if you remember it you can derive most of the knowledge of trigonometry.
For students, please remember that there is also a skill of trigonometry, which comes from repeatedly applying the knowledge. In particular, a lot of trig problems are only solvable if you recognize the different trig identities and use them to convert the form of an equation into something you can deal with. It's worthwhile to put in the practice so you can recognize these patterns.

[shreeniwaz]

I learnt trigonometry since highschool.. WHY DIDN'T THEY TEACH THIS EVER!? It's so easy and sensible in this way.. why!!??

[perrymaskell]

Suddenly the complimentary functions and the identities make so much sense. Brilliant way of showing all the trig functions.

[Alnakera]

I remember clearly back in highschool asking my teacher "what does the tan represent on the unit circle?" He said, it's just the ratio of sin and cos. Ever since then anything other than sin and cos were just equations and had no graphical meaning.

+10 years later, I finally got a legitimate answer. Thanks!

[jmscnny]

Holy crap. It has only taken me 60 years to stumble across this explanation.

[markdonnelly]

Imagine if every school took these functions to the simple basic level you just did in only a couple of minutes. There would be nothing scary about trig again. I wish it had all been expained so easily when I was at school. It took me to research it myself years later to understand trig. Great video.

[Thrakerzog]

You are by far a better teacher than ANY of the teachers at my old high school. In just over 4 minutes, you explained in a clear concise way the fundamentals of trigonometry. Thank you!

[SpencerWilliamsIV]

Jesus, no one has ever explained to me why that darn function is called tangent. Thank you.

[paulfrost]

I have a reasonable ability in mathematics. However to find out at the age of 61 that the co in cosine etc means complimentary is a revelation. I am somewhat surprised that that was never mentioned to me all those years ago “hay ho”. So just for that thank you very much.

[garrettbates]

I took trig in university, and understood it pretty well at the time. And I've seen the static version of this diagram, but it never really made sense to me because these functions were never taught to me this way, outside of sine and cosine.

This explanation was really cool and makes a ton of sense.

[RecOgMission]

From a nerd and someone with a decent level of maths education: This is brilliant! It makes so much sense out of these concepts, all in one connected image!

[QuantumAstrophile]

Incredibly helpful. It bridged geometry into trig for me. Trig makes so much sense now.

[VegaOfficiaI]

I sat in a 2 hour class not understanding a single thing, just for this visual to teach me in less than 5 minutes. thank you!

[mmeis]

As a mechanical draftsman in the 70/80s descriptive geometry using drawings technical methods was used similiar, but not knowing trig hurt my career. I had to relearn it starting with ratios...do they even teach this anymore.
Oscar Had A heap Of Apples saved my butt. sin = O/H cos=A/H tan=O/A and of course pythagoreus....A2+B2=C2
Your diagram just opened my eyes - and brought it all together. Very good Sir. KISS as we would say in designing: Keep it simple stupid. Thank you.

[randydewees]

LOL. I remember hitting the windshield in my 2nd Calculus class when I was suddenly confronted with the reality that I had either never learned the trig identities or had completely forgotten them. The prof was truly bad too, so instead of scrambling I decided to drop that class, review some basic math, and burned through the class the next semester. This vid might have saved the day, but this all happened in 1982.

[borisdorofeev]

I was thinking of these exact properties and interactions after seeing the static pictures and I knew some person must have animated this diagram which shows perfectly what these concepts really are.
One of the most elegant math videos I've seen on Youtube and I can't believe it's so recent.

[teacher_of_the_arcane]

Just remembering the agony of putting all that information into my usable knowledge !! Then remembering trying to teach that same info to my students for twenty years !! Saving and Sharing this. Blessings for the individual who put this together !

[robelbelay]

Mind Blown! First time grasping why these things are the case instead of pure memorization

[kennithlambert]

Your diagram really helped me with the infinity values by explaining it in simple terms like y and x never cross.
I've seen the same diagram in motion but slowing it down I was able to grasp more.