how I remember all the trig and inverse trig derivatives

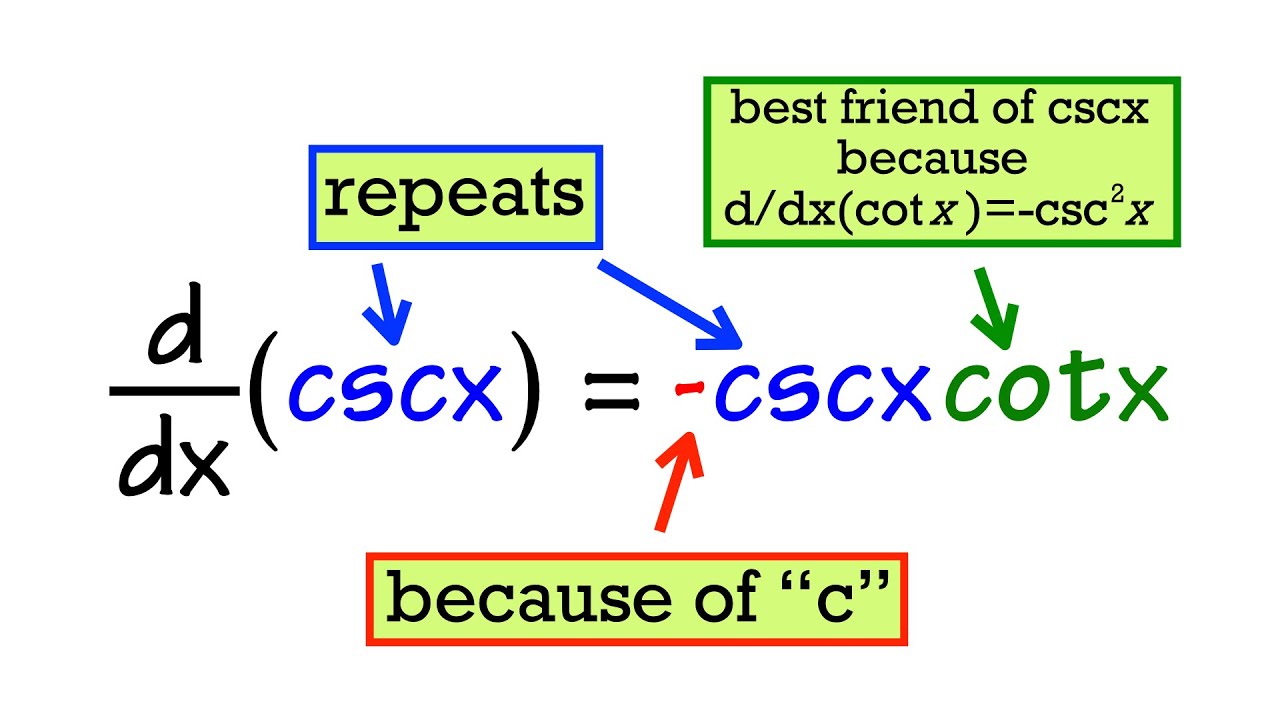
My tips for remembering the derivatives of trig functions & inverse trig functions. These are must-knows in Calculus 1 and AP Calculus AB. The main idea is to organize the functions in order so we can see a pattern more easily. Also doing lots of practice would help. Feel free to comment on your own way of remembering these derivatives in the comment section.

0:00 Derivatives for regular trig functions
3:18 Derivatives for inverse trig functions
5:22 The trig identities behind 1-x^2, 1+x^2 and x^2-1

-----------------------------
-----------------------------
#calculus #math #bprpcalculus

[essraateah]

Cool mic 🎤+cool explanation+cool math =coolest teacher 👨‍🏫!thank you, may allah reward you and guide us all

[arimermelstein]

I memorize only derivative of arcsin and arctan because they come up a lot. If you asked me to find any of the other ones, I would just reprove it with implicit differentiation.
Also, I don’t really like the identity way. When I have to go back from the theta world to the x world, I draw a right triangle to find the relationships.

[Kcite]

what an absolute legend, i was just struggling to remember these derivatives and saw this video. huge thanks for saving my grades!

[stantackett]

I must be showing my age. I was about to ask you for hints on how to define inverse cosine and cosine, because I'm reverting to my Amiga 500 using BASIC.

then I suddenly remembered e^ix and it all came back.

I'm 54, have degrees in math, computer science and nuclear engineering b I think it's time to retire if I can't remember simple math 😂

And I adore your channel. Like to refresh my skills watching you whoever possible. keep up the good work!!

[asdf]

Man you are the best, I have been having a hard time memorizing these but this just made it so much easier. Thank you so much from all of the struggling calculus students out there!

[liamwelsh]

The way my calc teacher showed us to remember it is using the letters SST. If you want the derivitive of sec, it's sec x tan x. S = S * T. For tan its sec x sec x. T = S * S. For CSC and COT, you do the exact same thing but just add the C and of course the negative. And for sin and cos, they're just opposites with cos being negative of course.

[ganeshpatwal]

You will definitely be useful to me next year. In 11th grade. :D

[heliocentric]

How I remember all the trig and inverse trig derivatives?
just calculus: Video 7:15 long.
FAST!: "Don't forget them"

[___aaron.m]

great video! the most useful to me was tan and sec are best friends same with cot csc

[justabunga]

For the derivatives of arcsec(x) and arccsc(x), shouldn't there be an absolute value around the x (i.e. 1/(|x|sqrt(x^2-1)) and -1/(|x|sqrt(x^2-1)))? I saw those in most of the textbooks.

[johnnolen]

I remember the trig derivatives by repetition. (If you do something 10 000 times, you're bound to remember it.) Also you can get the derivatives of sine and cosine simultaneously by differentiating Euler's formula. d[cos(x)]/dx = Re {d[e^(ix)]/dx} and d[sin(x)]/dx = Im {d[e^(ix)/dx}.

To figure out the derivatives of the inverse functions I use a reference triangle and the inverse function theorem together.

The reason for the absolute value in the derivative of arcsec(x) is because in order for arcsec(x) to be a function it has to be one - to - one. And if sec(y) = x then cos(y) = 1/x. If we differentiate this expression, we get - sin(y)·dy/dx = - 1/x^2. This implies dy/dx = 1/(x^2·sin(y)) = 1/(x^2·sqrt[1 - 1/x^2]) = 1/(|x|·sqrt[x^2 - 1]). ◼

[bruceu]

Thank you so much, this is going to save my ass from failing my calc 1 midterms next week. Could you do hyperbolic functions and their inverses derivatives?

[nkyxd]

Great It's so helpful for a cal 1 student like me😎😎

[justabunga]

We know that the derivatives of arccos(x), arccsc(x), and arccot(x) are negative versions of the derivatives of arcsin(x), arcsec(x), and arctan(x) (most likely used). The difference from there is that they are all off by the constant of pi/2. Adding a constant will have the derivative to be 0. Therefore, anytime the constant is off, the function always has the same derivative. You can try to integrate and see the difference from there.

[rody]

You could think of their syllables for derivatives of tanx and cotx.
2 syllables: tan-gent ==> se-cant
3 syllables: co-tan-gent ==> co-se-cant

[HomieSeal]

I’ve been trying to figure this out for months now, but I have a question: is this related to e^kx at all? In terms of the repeat and then the best friend. Is there some way to find *all* functions that follow the pattern $f’(x) = f(x)*g(x)$?

[anshumanagrawal]

I used to have ways to remember, but now with so much practice they are literally set in my brain like stone

[dominicellis]

Why are there no parabolic trig functions?

[aguy]

Can you please post calc 3 vids I am planning to learn it on my own

[randomxxvids]

Now make a video with derivatives of hyperbolic trig functions