filmov
tv
Calculus - Integral cosx e^ sinx and Integral sinx e^ cosx
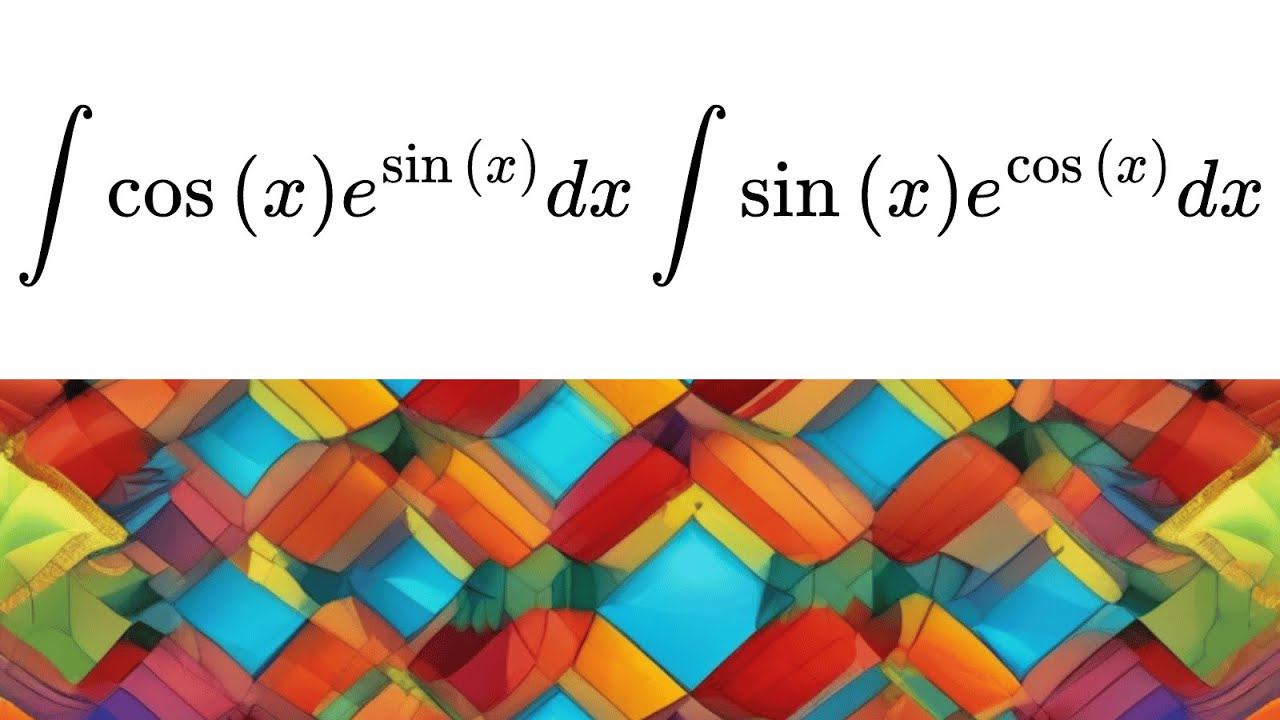
Показать описание
The integrals of functions involving trigonometric and exponential expressions can be quite intricate and fascinating. Let's delve into the integrals of \( \cos(x) e^{\sin(x)} \) and \( \sin(x) e^{\cos(x)} \).
1. **Integral of \( \cos(x) e^{\sin(x)} \)**:
The integral of \( \cos(x) e^{\sin(x)} \) can be approached using a substitution method. Let \( u = \sin(x) \). Then, \( du = \cos(x) dx \). This transforms the integral into a more straightforward form:
\[ \int \cos(x) e^{\sin(x)} dx = \int e^u du. \]
The integral of \( e^u \) is simply \( e^u \). Therefore, substituting back \( u = \sin(x) \), we get:
\[ \int \cos(x) e^{\sin(x)} dx = e^{\sin(x)} + C, \]
where \( C \) is the constant of integration.
2. **Integral of \( \sin(x) e^{\cos(x)} \)**:
Similarly, for the integral of \( \sin(x) e^{\cos(x)} \), we also use a substitution approach. Let \( u = \cos(x) \). Then, \( du = -\sin(x) dx \), which means \( -du = \sin(x) dx \). Substitute these into the integral:
\[ \int \sin(x) e^{\cos(x)} dx = \int -e^u du. \]
The integral of \( -e^u \) is \( -e^u \). Substituting back \( u = \cos(x) \), we obtain:
\[ \int \sin(x) e^{\cos(x)} dx = -e^{\cos(x)} + C, \]
where \( C \) is the constant of integration.
In summary, the integrals of these functions leverage the power of substitution to simplify the integration process, yielding elegant results that combine trigonometric and exponential functions.
1. **Integral of \( \cos(x) e^{\sin(x)} \)**:
The integral of \( \cos(x) e^{\sin(x)} \) can be approached using a substitution method. Let \( u = \sin(x) \). Then, \( du = \cos(x) dx \). This transforms the integral into a more straightforward form:
\[ \int \cos(x) e^{\sin(x)} dx = \int e^u du. \]
The integral of \( e^u \) is simply \( e^u \). Therefore, substituting back \( u = \sin(x) \), we get:
\[ \int \cos(x) e^{\sin(x)} dx = e^{\sin(x)} + C, \]
where \( C \) is the constant of integration.
2. **Integral of \( \sin(x) e^{\cos(x)} \)**:
Similarly, for the integral of \( \sin(x) e^{\cos(x)} \), we also use a substitution approach. Let \( u = \cos(x) \). Then, \( du = -\sin(x) dx \), which means \( -du = \sin(x) dx \). Substitute these into the integral:
\[ \int \sin(x) e^{\cos(x)} dx = \int -e^u du. \]
The integral of \( -e^u \) is \( -e^u \). Substituting back \( u = \cos(x) \), we obtain:
\[ \int \sin(x) e^{\cos(x)} dx = -e^{\cos(x)} + C, \]
where \( C \) is the constant of integration.
In summary, the integrals of these functions leverage the power of substitution to simplify the integration process, yielding elegant results that combine trigonometric and exponential functions.
 0:02:15
0:02:15
 0:00:43
0:00:43
 0:01:00
0:01:00
 0:11:16
0:11:16
 0:07:52
0:07:52
 0:04:08
0:04:08
 0:02:27
0:02:27
 0:10:10
0:10:10
 0:02:48
0:02:48
 0:10:36
0:10:36
 0:00:09
0:00:09
 0:10:02
0:10:02
 0:01:56
0:01:56
 0:03:57
0:03:57
 0:07:04
0:07:04
 0:07:30
0:07:30
 0:22:40
0:22:40
 0:16:40
0:16:40
 0:11:30
0:11:30
 0:07:16
0:07:16
 0:40:04
0:40:04
 0:13:58
0:13:58
 0:26:06
0:26:06
 0:03:50
0:03:50