filmov
tv
Integral of e^(ax)sin(bx) by using complex numbers (beyond calculus 2)
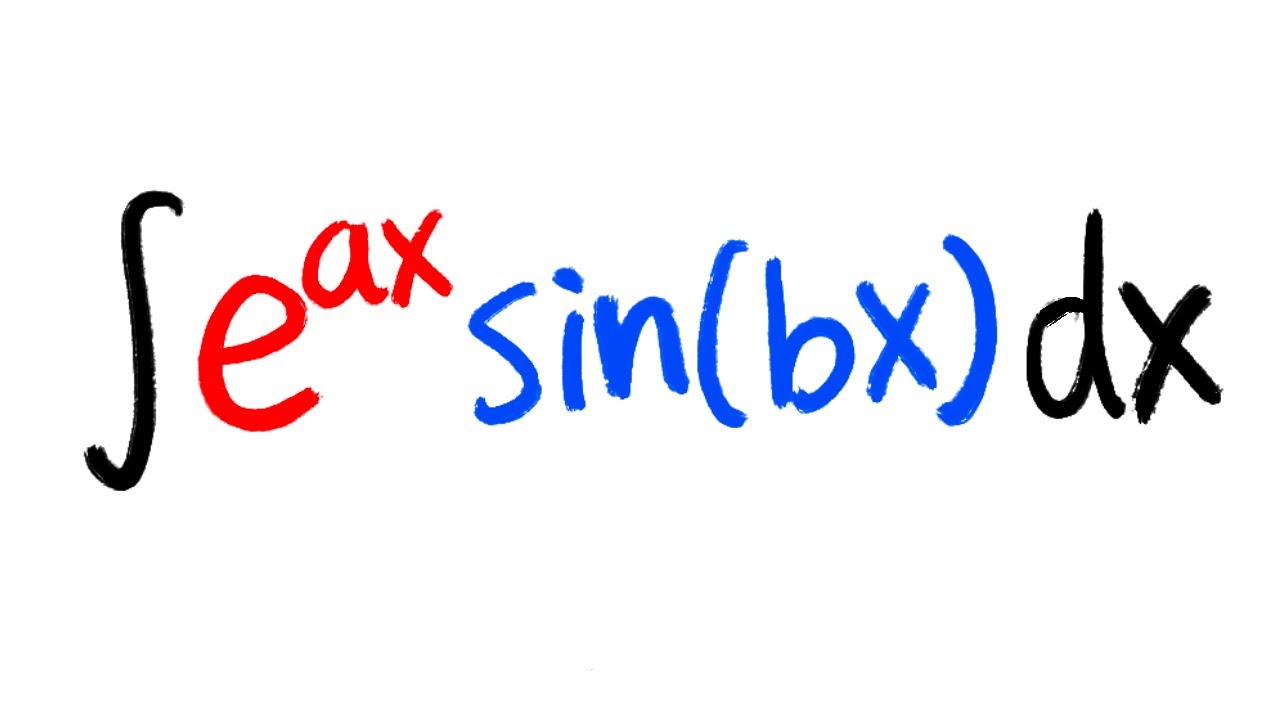
Показать описание
Calculus tutorial on the integral of e^(ax)*cos(bx) and integral of e^(ax)*sin(bx), no integration by parts but we will use complex numbers. Whenever we have an exponential function e^x and a sine or cosine function, we can use integration by parts or this complex number method.
Integral of e^(ax)sin(bx) by using complex numbers (beyond calculus 2)
Integral of (e^ax)sin(bx) (by parts + by parts)
Integral of e^ax sin bx | Integration by parts
Class 12th – Integral of e^ax sin bx dx | Integrals | Tutorials Point
Integral e^(ax)sin(bx) two ways to compute
Integrate of the form ∫ e^ax sin bx dx and ∫ e^ax cos bx dx
Integration of e^ax sin bx and e^ax cos bx
#Integrationbyparts || Evaluate integral of e^{ax}\sin{bx}
Integrate e^ax sin bx dx | Integration of e^ax sin bx | Integral of e^ax sin bx dx | #e^axsin bx
`int e^(ax)sin bx dx=` | Class 12 Maths | Doubtnut
Integral of form `e^(ax) sin bx dx` or `e^(ax) cos bx dx`
#Integrationbyparts || Evaluate integral 0 to infinity of e^{-ax}\sin{bx}
Integrals of type e^(ax)Sin(bx) and e^(ax)Cos(bx) (@romualdorebello4629)
Integral of e^ax cos(bx) and Integral of e^ax sin(bx) no integration by part
Integration of e^ax Sin bx and e^ax Cos bx - Indefinite Integration | Class 11/12/IIT-JEE Maths
Integral of e^(ax)sin(bx + c)
Int e^(-ax) Cos(bx) dx from 0 to infty
ANTI DERIVATIVE-1 , HOW TO FIND ANTIDERIVATIVE exp(ax) sin bx and exp(bx) cos bx EASIER
Evaluate the integral of e^ax sin(bx+c)
Integral Practice #28: integral of (e^(ax)sin(bx))dx (intgration by parts)
Integration of Exponential Functions - Integral of e^ax*cos(bx) and sin(bx) (Lect. 7)
Avoiding integration by parts: e^(ax)sin(bx)
INTEGRATION SHORTCUT OF ∫eax sin(bx+c)dx or ∫eax cos(bx+c)dx
nth derivative of e ^ax.sin(bx+c) ||Successive differentiation of e ^ax.sin(bx+c) ||
Комментарии
 0:10:36
0:10:36
 0:07:19
0:07:19
 0:11:13
0:11:13
 0:01:44
0:01:44
 0:12:31
0:12:31
 0:15:23
0:15:23
 0:04:50
0:04:50
 0:06:14
0:06:14
 0:08:26
0:08:26
 0:06:16
0:06:16
 0:07:59
0:07:59
 0:06:14
0:06:14
 0:18:36
0:18:36
 0:08:37
0:08:37
 0:25:22
0:25:22
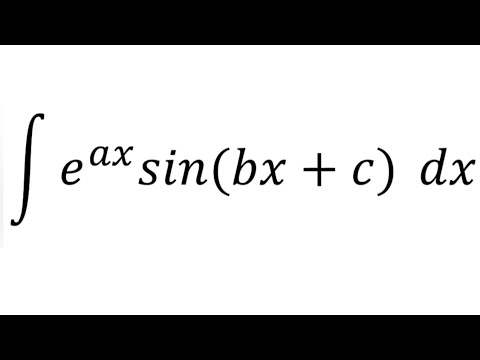 0:04:00
0:04:00
 0:09:21
0:09:21
 0:14:45
0:14:45
 0:06:50
0:06:50
 0:05:57
0:05:57
 0:38:37
0:38:37
 0:17:00
0:17:00
 0:03:00
0:03:00
 0:11:40
0:11:40