filmov
tv
This integral will improve your advanced math skills

Показать описание
A beautiful integral solved using Feynman's technique and complex numbers. Full solution development leading to a result involving pi and the euler mascheroni constant.
My complex analysis lectures:
If you like the videos and would like to support the channel:
You can follow me on Instagram for write ups that come in handy for my videos and DM me in case you need math help:
My LinkedIn:
Advanced MathWear:
My complex analysis lectures:
If you like the videos and would like to support the channel:
You can follow me on Instagram for write ups that come in handy for my videos and DM me in case you need math help:
My LinkedIn:
Advanced MathWear:
This integral will improve your advanced math skills
This Integral Will Make You Better At Calculus
What my calculus 2 students did to this integral!
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
Learn to Solve an Integral (What Makes You Beautiful Parody) AP Calculus BC
What is Integration? 3 Ways to Interpret Integrals
The Most Useful Calculus 1 Tip!
The truth about dating 😂 #couple #couplegoals #husbandwife #comedy #wife #husband #relationship
Emotional Integration & Healing #lifecollagejournals #journaling #stevenstanchallenge
Why is there a Pi (π) in This Gaussian Integral?
3-2-1 STUDY METHOD
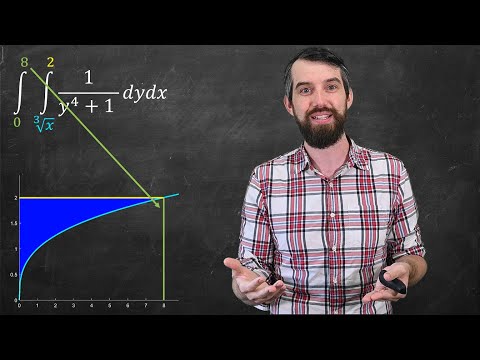
Change the order of integration to solve tricky integrals
DO NOT use ChatGPT - How to use AI to solve your maths problems ✅ #chatgpt #wolframalpha
What Integration Technique Should I Use? (trig sub, u sub, DI method, partial fractions) calculus 2
Differentiation and Integration formula
Finding the Area Between Two Curves by Integration
Change of Variables & The Jacobian | Multi-variable Integration
How to Get Over Your Social Anxiety
Definite Integral
Only FEYNMAN'S TRICKS can help solve this TERRIFYING INTEGRAL
Simple Integral vs Double Integral #calculus #maths
This trick can make your rubik's cube 2x faster😱🔥#ytshorts#shorts#drcuber
IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit
✏️ Integrate Figma in your editor #shorts #vscode #coding #extensions #programming #2099 #tips #js...
Комментарии
 0:09:54
0:09:54
 0:05:59
0:05:59
 0:00:25
0:00:25
 0:00:09
0:00:09
 0:03:39
0:03:39
 0:10:55
0:10:55
 0:00:10
0:00:10
 0:00:31
0:00:31
 0:00:08
0:00:08
 0:08:37
0:08:37
 0:00:08
0:00:08
 0:07:39
0:07:39
 0:00:14
0:00:14
 0:22:40
0:22:40
 0:00:06
0:00:06
 0:07:52
0:07:52
 0:10:07
0:10:07
 0:00:32
0:00:32
 0:11:05
0:11:05
 0:14:17
0:14:17
 0:00:50
0:00:50
 0:00:16
0:00:16
 0:00:12
0:00:12
 0:00:09
0:00:09