Change the order of integration to solve tricky integrals

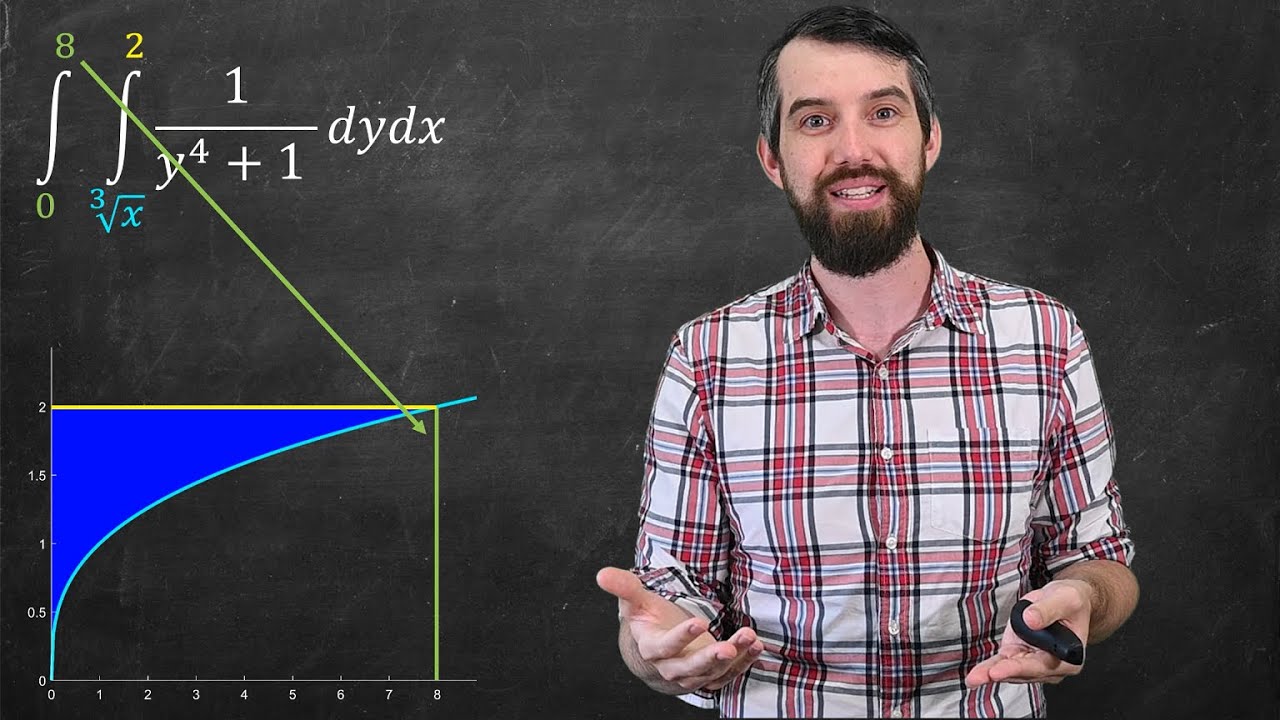
The double integral over a region can be expressed in two different ways. It could be that we write dxdy which means that we integrate with respect to x first and then y (called horizontal strip). Or it could be dydx which means y is integrated first and then x (vertical strips). The big idea is we can convert between these and so can choose whichever is the easier of the two. The steps are:
1) Given an integral, sketch the region implied by the limits of integration
2) Now interpret that region the opposite way, such as vertical strips instead of horizontal strips
3) Write the new integral in the opposite order of integration
4) Hopefully it will now be easier to compute!

****************************************************
COURSE PLAYLISTS:

***************************************************

► Want to learn math effectively? Check out my "Learning Math" Series:

►Want some cool math? Check out my "Cool Math" Series:

****************************************************

*****************************************************

This video was created by Dr. Trefor Bazett. I'm an Assistant Teaching Professor at the University of Victoria.

BECOME A MEMBER:

MATH BOOKS & MERCH I LOVE:

[angelluisgarciaguzman]

To get the YT algorithm working: Just add Calculus III and the title and tags

[shubhamingale]

I wasn't understanding how to assign the values of limits and I was worried about it as my exams are approaching. Now I have understand it clearly Thank you Dr. Bazett, you are a life saver. Love from India.

[NielsLeoLarsen]

This man will single handed save my calculus journey.

[Ann-nyyb]

This video gives me hope. I was on the verge of breaking into molecules as I did not understand a single word from my Instructor when he explained this. Thank you very much, and now I get it.

[tomatrix]

I’m so glad I stumbled upon this channel, it’s a gold mine. Great work!

[duartegomes]

I am serious. Thank you, i am an ee student and my professor just taught us how to do this very fast like everyone would know. you're a king, God bless u

[isuckatthisgame]

The hardest part, I've found, is to know how to plot these functions in order to see where is the region you want to integrate. I need to build geometric intuition.

[fatherkeys]

You explained this so clearly. I’m so happy I found this channel for calc 3

[viliusr]

Man you opened my eyes and i finally can understand the logic behind this. That's very great teaching

[briandwi]

Sometimes maths really is like magic! Such a wonderful technique. Thanks for the video. Pure class.

[mohandoshi]

Superb explanation and very succinct too. Great video Dr. Bazett.

[ReidCipriani]

Thank you. This concept is simple yet hard to visualize sometimes

[luna_lovegood]

Omg this saved my life!!!! thankyou so much, i had so much trouble visualizing the inner and outer parts on a diagram and now i understand

[namhoang]

great video. All other instruction videos did not go as deep to the basis as this one, I can say for sure.

[Aimsixmeals]

Something needed now that everything is online due to corona until next year

[hdot]

Hi Dr Trefor Bazett. Thanks for the great explanation and solid visuals!

I'm a little confused on one part and was hoping you could help clear up my misunderstanding 😁

Why is the upper bound on the inner x integral y^3 and not 8?

We have the line x=8 plotted and it's equivalent to 2^3.

Why can we not argue that the largest x value of the shaded area is 8 instead of y^3?

[monicapym]

Great video and explanation!! Thank you!!

[JamesLewis]

It's not obvious, but the factorization of y^4+1 over the reals is (y^2−y√2+1)(y^2+y√2+1); it's the difference of the two squares (y^2+1)^2 and 2y^2.

Of course, if you then use partial-fraction decomposition and complete the square and find an antiderivative, you'll end up with a sum of logs and arctans that would be unusually difficult to work with, and *then* you would need to deal with the compositions of those functions with the cube root to calculate the outer integral.

To spell it out more, it turns out that an antiderivative of 1/(y^4+1) is evaluated at the upper limit, this is sqrt(2)/8*(2pi-2arctan(2sqrt(2)/3)+ln((33+20sqrt(2))/17)), and it turns out that when you evaluate it at the lower limit, the resulting function of x *does* have an elementary antiderivative, but it's far from obvious, and it also is far from obvious that every term cancels except for a couple of terms that add up to ¼ln(17).

[diveintoengineering]

Thank you! Please keep uploading such wonderful videos!

[mister_allmond]

Very thorough tutorial!!! Enjoyed watching!