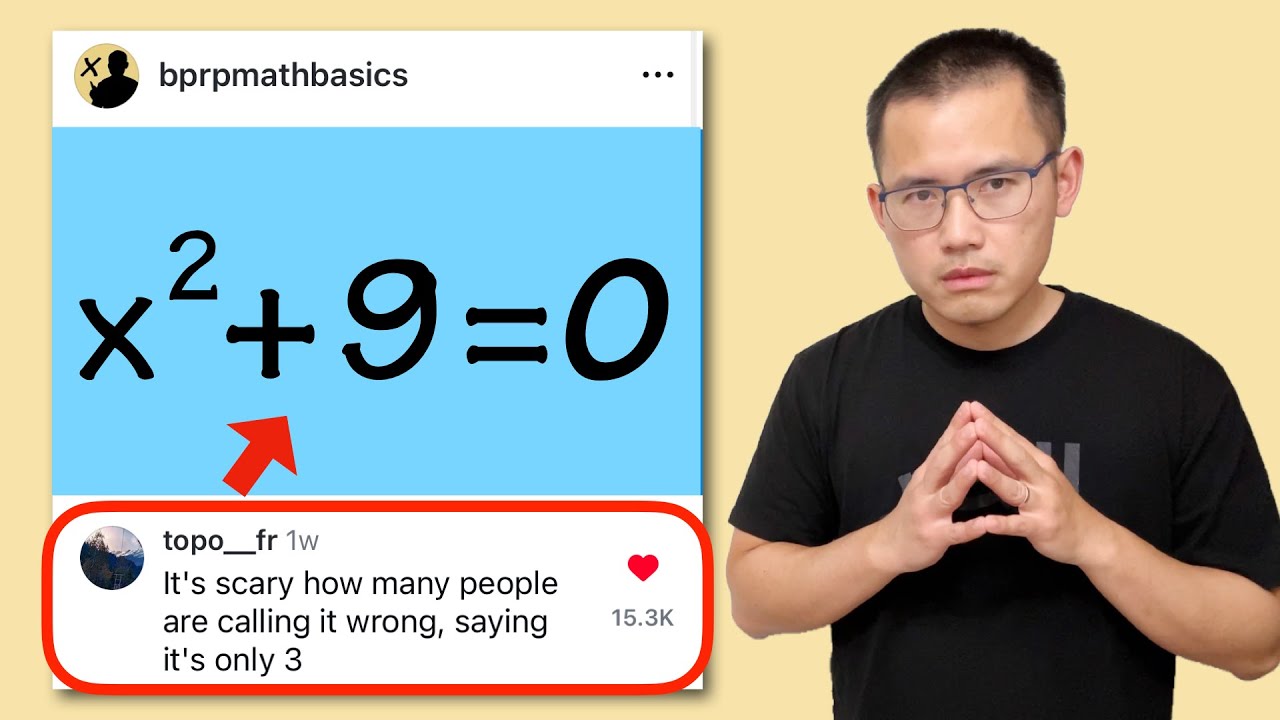
'It's scary how many people are calling it wrong, saying it's only 3'

How do we solve the quadratic equation x2+9=0? Does this quadratic equation have real solutions? Some of my Instagram reel viewers don't believe that x2+9=0 can be solved. Today, I will show you two approaches for solving x2+9=0: taking the square roots on both sides and factoring.

0:00 Solving x^2+9=0 by taking the square roots on both sides
1:36 Solving x^2+9=0 by factoring

-----------------------------
-----------------------------
#math #algebra #mathbasics

[antilles]

As fun as it is for me to revisit high school & college math with these videos, the thing that leaves me most impressed and entertained is watching him seamlessly switch dry erase colors on the go like it's nothing.

[Stub.]

I like that shirt.
It's "algebra" in Arabic for anyone wondering.

[samwilde]

It is so sstisfying how he can seamlessly swap between the black and red marker as he writes

[LordAziki]

I'm curious to see how people incorrectly solved for x=3 without realizing something was off when the equation simplified to 18=0. Assuming they weren't aware of i, it would make far more sense to conclude there is no solution.

[jimbobago]

I prefer using your second method because it makes certain I get both solutions. As a tutor, forgetting the plus/minus seems too common. Also students get confused about why we need both values when solving an equation but only use the principal root in other square root problems; if I just factor, it’s a non-issue.

[richbaird]

Imaginary doesn't mean pretend it means it follows a different set of rules than the so called real numbers you're used to. The imaginary unit i is defined to be the square root of -1 and from that definition comes a whole lot of extremely useful properties for science and engineering. These numbers may behave differently from the reals but that doesn't make them pretend.

[reaper]

My initial reaction: "but... you can't negative a square"

[NecroknightZ]

Thank you for the throwback to math lessons! It might not have been enjoyable back then, but I'm glad I still got the correct answer!

[michasokoowski]

i dislike the sentence "not in the real world" because there are imaginary numbers in physic models...

[killer]

That t-shirt, that poster in the back and writing with two marker i like it all

[ned]

Because voltage is tension or pressure, it's expressed as tension or negative tension.
When else are "imaginary" numbers used in the real world?

[lilmayrose]

You absolutely blew my mind with the factoring solution. I've ALWAYS been forgetting to do +/- when I take the sqrt of both sides in my college math courses, but showing it here as a result of factoring is going to help me remember for sure! Also showing that even adding a quadratic can be interpreted as the difference of squares, just minus a negative number was a paradigm shift for me.

[turboskarner]

This mans marker skills are still so slick, plus thank you for explaining the +- part, never seen it written out

[dd-dimz]

I'm used to seeing you tackle more difficult stuff, this is a nice change of pace.
Is what I would have said if I didn't notice that this is a different channel with a basics behind the main name. 😅

[Omni]

I've never seen someone think of natural numbers as squares of complex numbers, that's amazing!

[eggsnham.]

huh, I never thought of using i the way you used it in the second method. I always saw it as just a notation formality of sorts for negative square roots. That's honestly pretty cool!

[shipsahoy]

Good work; your algebraic manipulations are absolutely correct .. finally somebody who knows what they're talking about with this type of mathematics .. there's only one thing here though, that I'd like to point out ..
I wouldn't phrase it as "not being in the real world"
bc we would not be able to explain many things mathematically in branches of physics that actually are real world phenomena without the i operator at our disposal ...
in electrical concepts, it would create difficulty, although we use j instead of i, but everything else about the operator itself remains consistent. Mathematicians use i for the square root of -1, which creates 4 useful identities when considering i to be raised to the second, third, and fourth powers.
Have a great day!

[dunngunkadoid]

Dude did the impossible and made math legitimately interesting for me to watch/listen to. Mad respect man, keep up the great work.

[AnjiEnnui]

Oh my goodness the way he seamlessly transitions from black to red is really satisfying.

[sentientlvl.mortar]

Was already screaming "±3i" when I saw the thumbnail