filmov
tv
Ch 5: What are Dirac deltas and wavefunction inner products? | Maths of Quantum Mechanics

Показать описание
Hello!
This is the fifth chapter in my series "Maths of Quantum Mechanics." In this episode, we'll dig into what the Dirac delta is and how we should understand it as physicists. We'll then use it to show where the inner product for wavefunctions comes from.
If you have any questions or comments, shoot me an email at:
Thanks!
Animations:
All animations created by me within Python, using Manim. To learn more about Manim and to support the community, visit here:
Music:
--------------------------------------------------------------
♪ 35 by HOME
--------------------------------------------------------------
This is the fifth chapter in my series "Maths of Quantum Mechanics." In this episode, we'll dig into what the Dirac delta is and how we should understand it as physicists. We'll then use it to show where the inner product for wavefunctions comes from.
If you have any questions or comments, shoot me an email at:
Thanks!
Animations:
All animations created by me within Python, using Manim. To learn more about Manim and to support the community, visit here:
Music:
--------------------------------------------------------------
♪ 35 by HOME
--------------------------------------------------------------
Ch 5: What are Dirac deltas and wavefunction inner products? | Maths of Quantum Mechanics
How did Dirac discover the Dirac Equation #Shorts
Deriving the Dirac Equation
Ch 6: What are bras and bra-ket notation? | Maths of Quantum Mechanics
Dirac Delta Function - How does it work? | Maths of Quantum Mechanics
Mathematics For Physics, Ch5.1: the Dirac Delta
Mathematics For Physics, Ch5.2: Two Definitions Of the Dirac Delta
Bsc 1st Semester Physics Chapter-5: Introduction to dirac delta function
Dirac's Delta Function
Demystifying the Dirac Delta - #SoME2
Dirac Notation (Lecture 5)
BEGINNERS GUIDE: Dirac Live Room Correction for HiFi
Physics Ch 67.1 Advanced E&M: Review Vectors (102 of 113) The Dirac Delta Function is NOT a Func...
Pregnancy diagnosis l Dr umar khan
What is Dirac Equation | Dirac Equation Explained | Dirac Equation for Beginners
UPSC VS IIT JEE 🥵 #iitstatus #motivation #toppers #iitjee #jeemains #upscstatus #neet #nit #jee
What is Dirac Equation | Dirac Equation Explained | Dirac equation in relativistic quantum mechanics
What is Dirac Equation | Dirac Equation Explained | Dirac Equation In Relativistic Quantum Mechanics
What is Dirac Equation | Dirac Equation Explained | Dirac Equation #shorts #youtubeshorts
Physics Ch 67.1 Advanced E&M: Review Vectors (112 of 113) Integrate Dirac Delta Functions (Part ...
AP Scores are out today
Physics Ch 67.1 Advanced E&M: Review Vectors (101 of 113) The Dirac Delta Function is Useless? B...
The Schrödinger Equation Explained in 60 Seconds
Brian Cox explains quantum mechanics in 60 seconds - BBC News
Комментарии
 0:10:31
0:10:31
 0:01:00
0:01:00
 0:16:34
0:16:34
 0:10:03
0:10:03
 0:16:57
0:16:57
 0:19:53
0:19:53
 0:17:18
0:17:18
 0:01:51
0:01:51
 0:09:10
0:09:10
 0:09:22
0:09:22
 0:24:26
0:24:26
 0:19:56
0:19:56
 0:02:14
0:02:14
 0:00:20
0:00:20
 1:00:19
1:00:19
 0:00:14
0:00:14
 0:37:31
0:37:31
 0:30:00
0:30:00
 0:00:58
0:00:58
 0:05:38
0:05:38
 0:00:51
0:00:51
 0:04:31
0:04:31
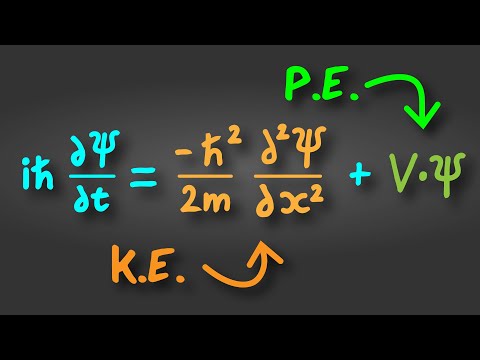 0:01:00
0:01:00
 0:01:22
0:01:22