filmov
tv
Solving An Exponential with Lambert's W
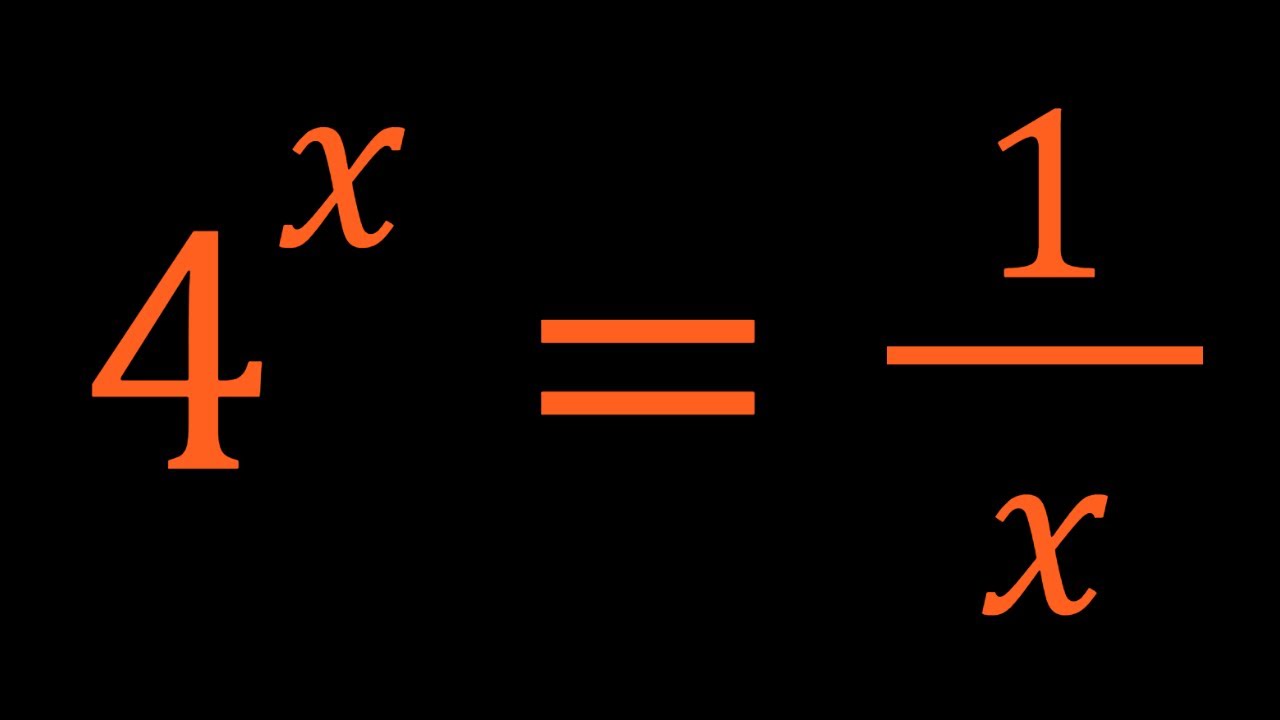
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations #Exponentials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations #Exponentials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Lambert W Function solving exponential equations
Lambert W Function
A Golden Exponential Equation Using Lambert W Function | Math Olympiad
How to Apply Lambert W Function To Solve Exponential Equations With Variables in the Base & Expo...
Simple Yet Difficult. How to Solve Using Lambert W Function
How To Solve Exponential Equation x^5=9^x || Solving Exponential Equations.
You can solve unsolvable exponential equation 2x-4=2^x using Lambert W function.
Solving Exponential Equation 5^2x=7x Using Lambert Wn Function | Lambert w function introduction
how to solve maths problems quickly | math olympiad questions class 10 | maths olympiad class 11
Solving an Exponential Equation using Lambert's W
When mathematicians get bored (ep1)
A Nice Math Olympiad Exponential Equation 3^x = X^9
The famous exponential equation 2^x=2x (ALL solutions)
Solving 8 Equations w/ Lambert W function
Solving Exponential Equation Having Variable Exponents | Challenging Exponential Equation.
Lambert W Function vs GLOG Function / Which is better?
How REAL Men Integrate Functions
Germany | Math Olympiad Algebra Problem | A nice Lambert W Function | Can you solve this ? #index
PROBLEM ON LAMBERT W FUNCTION [ALMOST IMPOSSIBLE EXPONENTIAL EQUATION].
A Nice Exponential Math Problem | Lambert W Function | Olympiad
A Nice Exponential Equation, x²=2ˣ
Cracking the Toughest OLYMPIAD Exponential Problem with Logarithms and Lambert W Function| X=?
Exponential Functions 11^9x+11=9^11 | Solving Exponential Equations Using Logarithms.
Fear No Equation
Комментарии
 0:06:06
0:06:06
 0:14:35
0:14:35
 0:11:43
0:11:43
 0:10:20
0:10:20
 0:03:39
0:03:39
 0:11:56
0:11:56
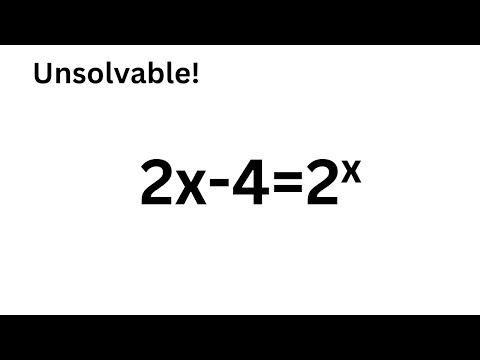 0:06:47
0:06:47
 0:10:06
0:10:06
 0:08:02
0:08:02
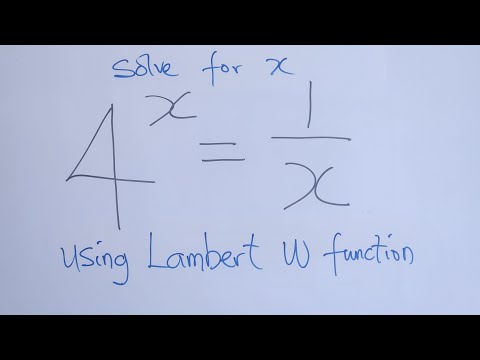 0:08:26
0:08:26
 0:00:37
0:00:37
 0:02:34
0:02:34
 0:10:28
0:10:28
 0:40:26
0:40:26
 0:10:35
0:10:35
 0:10:32
0:10:32
 0:00:35
0:00:35
 0:08:06
0:08:06
 0:34:02
0:34:02
 0:04:01
0:04:01
 0:10:34
0:10:34
 0:10:16
0:10:16
 0:06:22
0:06:22
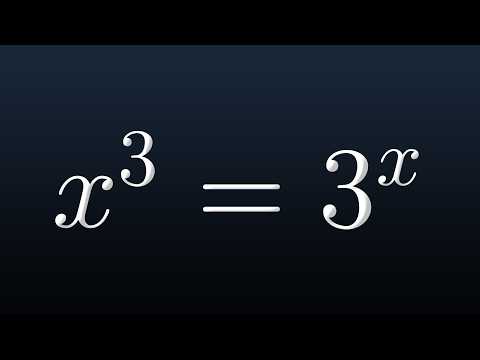 0:08:46
0:08:46