filmov
tv
How to find the antiderivative with fractions
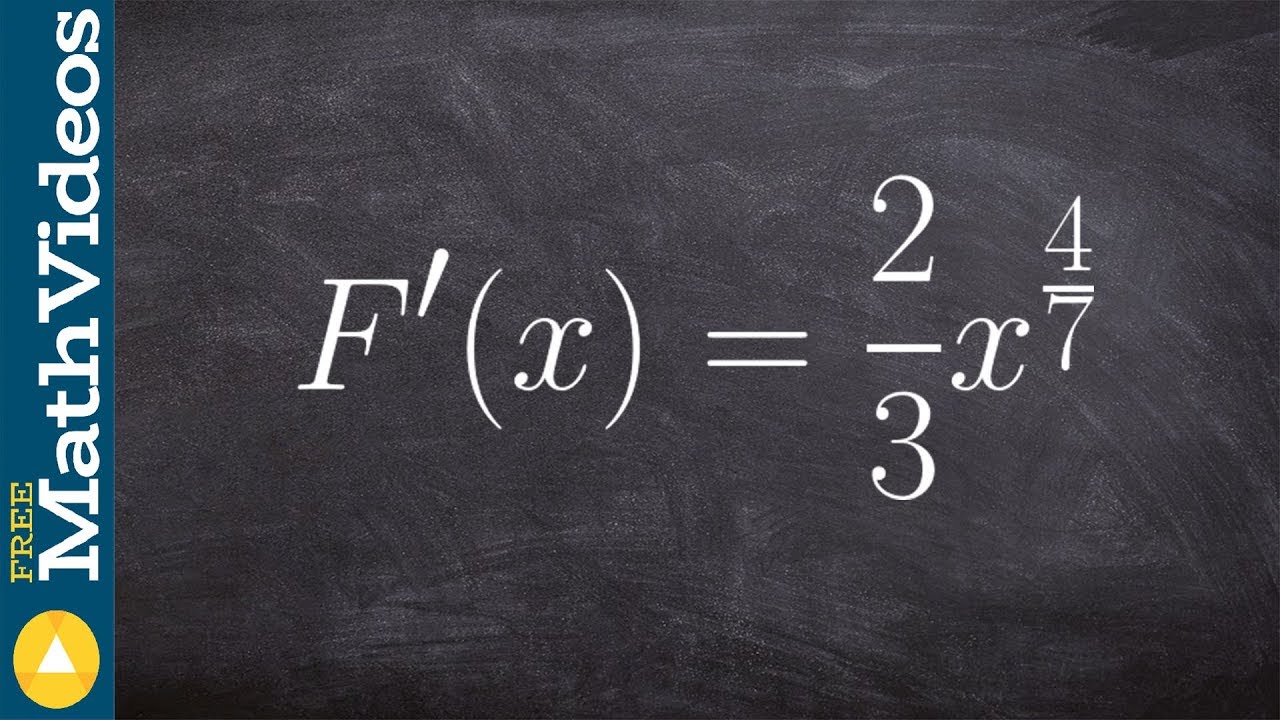
Показать описание
👉 Learn how to find the antiderivative (integral) of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which the upper and the lower limits/boundaries are known, otherwise the integral is indefinite. There are various formulas, depending on the function, and methods used in evaluating the integral of a function.
Organized Videos:
✅The Integral
✅Riemann Sum Approximation
✅Evaluate Integrals
✅Find the Particular Solution
✅Find The Integral of The Expression
✅Evaluate Using The Second Fundamental Theorem of Calculus
✅Trapezoid Area Approximation
✅Integration | Learn About
✅Separated Integrals Integration
✅Find The Average Value of a Function
✅Find the Antiderivative of a Function
Connect with me:
#integration #brianmclogan
Organized Videos:
✅The Integral
✅Riemann Sum Approximation
✅Evaluate Integrals
✅Find the Particular Solution
✅Find The Integral of The Expression
✅Evaluate Using The Second Fundamental Theorem of Calculus
✅Trapezoid Area Approximation
✅Integration | Learn About
✅Separated Integrals Integration
✅Find The Average Value of a Function
✅Find the Antiderivative of a Function
Connect with me:
#integration #brianmclogan
Antiderivatives
How to find the antiderivative of a simple function
Antiderivatives and indefinite integrals | AP Calculus AB | Khan Academy
Antiderivatives
How to find the antiderivative of a rational expression
Learn how to find the antiderivative of a polynomial
Calculus 1 - Integration & Antiderivatives
Integration (Calculus)
|| Integration || Class 12 Maths || NCERT Chapter 7 L-2 || #studyway
Visually determining antiderivative | AP Calculus AB | Khan Academy
How to find the antiderivative with fractions
Basic Integration... How? (NancyPi)
Calculus SPEEDRUN (U-Sub)!!
Find The Integral – How To Do Basic Calculus Integration
Find the general antiderivative of an algebraic function
What does area have to do with slope? | Chapter 9, Essence of calculus
How To Integrate Using U-Substitution
Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
How to find an antiderivative of a trig expression using identities
How to Find the Antiderivative or Indefinite Integral (Reverse Power Rule)
Find the Most General Antiderivative of 8x^9 - 3 - 3x^6 + 12x^3 Check answer by differentiation.
How to find the antiderivative using a negative exponent
Find the general antiderivative of a trigonometric function
What is Integration by Parts - How to do Integration by Parts
Комментарии
 0:33:50
0:33:50
 0:01:33
0:01:33
 0:03:43
0:03:43
 0:05:47
0:05:47
 0:01:48
0:01:48
 0:02:57
0:02:57
 0:40:04
0:40:04
 0:07:04
0:07:04
 1:43:21
1:43:21
 0:04:27
0:04:27
 0:02:20
0:02:20
 0:15:37
0:15:37
 0:01:00
0:01:00
 0:11:08
0:11:08
 0:02:11
0:02:11
 0:12:39
0:12:39
 0:21:35
0:21:35
 0:20:46
0:20:46
 0:01:27
0:01:27
 0:15:27
0:15:27
 0:03:01
0:03:01
 0:01:50
0:01:50
 0:01:36
0:01:36
 0:03:57
0:03:57