filmov
tv
PEMDAS Math Problem (Algebra Problem that Most People Get Wrong!) #shorts #maths #mathtricks

Показать описание
In this video I go over a Viral Math Problem that most People Get Wrong and explain how to solve it correctly by properly using the Order of Operations or PEMDAS. And even though this problem looks very simple over 70 percent of people get it wrong.
PEMDAS Math Problem | Algebra Fundamentals | JusticeTheTutor #math #shorts #maths #mathstricks
PEMDAS Math Problem | Algebra Fundamentals #math #mathtricks #shorts #maths
Do you know the Order of Operations? #pemdas #mathtutor #shorts #basicmath
Can you solve this equation?
PEMDAS Math Problem (Algebra Problem that Most People Get Wrong!) #shorts #maths #mathtricks
Viral Math Problem on PEMDAS Method
PEMDAS | Viral math problem
PEMDAS Viral Math Problem | Algebra Fundamentals | #Math #shorts #mathtricks #maths
Math Prof answers 6÷2(1+2) = ? once and for all ***Viral Math Problem***
Order of Operations with Parentheses and Exponents | PEMDAS | Math with Mr. J
Math Quiz #mathpuzzle #pemdas #shorts #mathquiz
Algebra. #mathshorts #bodmas #pemdas #algebra
Viral Math Problem || PEMDAS Rule #shorts #viral
Viral math problem | PEMDAS rule | Order of operations
PEMDAS!!! #orderofoperations #pemdas #maths #teacher
Right way of using PEMDAS or BODMAS. #algebra #mathshorts
Viral math problem #pemdas #viralmathproblem #mathematics #maths #math #shorts #short
PEMDAS Math Problem | Algebra Fundamentals #math #shorts#maths #mathtricks
PEMDAS / BODMAS Math Problem | Algebra Fundamentals GuinnessAndMathGuy #learnonyoutube
My two-year-old is solving math problems with the PEMDAS rule.
PEMDAS is wrong
Interesting Algebra Problem | PEMDAS and BODMAS | College Entrance Exam
PEMDAS RULE #pemdas
Algebra (PEMDAS Math Problem) #shorts #math #mathtricks
Комментарии
 0:00:29
0:00:29
 0:00:26
0:00:26
 0:00:58
0:00:58
 0:00:28
0:00:28
 0:00:49
0:00:49
 0:00:22
0:00:22
 0:00:54
0:00:54
 0:00:16
0:00:16
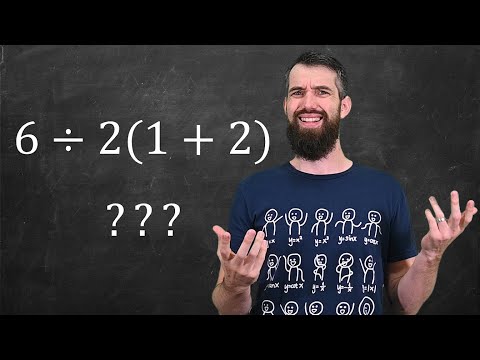 0:06:04
0:06:04
 0:06:42
0:06:42
 0:00:11
0:00:11
 0:00:11
0:00:11
 0:00:24
0:00:24
 0:00:09
0:00:09
 0:00:36
0:00:36
 0:00:14
0:00:14
 0:00:27
0:00:27
 0:00:23
0:00:23
 0:00:32
0:00:32
 0:00:43
0:00:43
 0:08:12
0:08:12
 0:03:34
0:03:34
 0:00:10
0:00:10
 0:00:41
0:00:41