filmov
tv
Proving the Formula for the Angle Between Two Vectors

Показать описание
Proving the Formula for the Angle Between Two Vectors
How To Prove The Quadratic Formula By Completing The Square
Learn how to use mathematical induction to prove a formula
Proving the Quadratic Formula - Twice (Precalculus - College Algebra 20)
proving the vertex formula of a parabola by using calculus
quadratic formula (the easiest way to prove it)
Proving the pq formula for solving quadratic equations
Art of Problem Solving: Proving the Quadratic Formula
How to prove the quadratic formula by completing squares
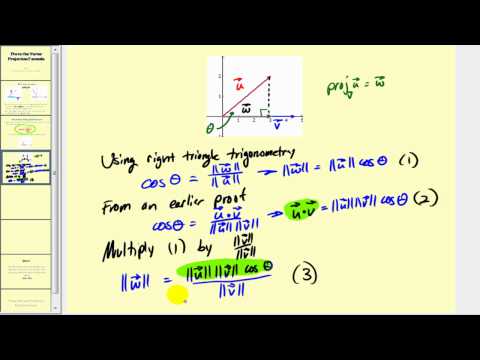
Proving the Vector Projection Formula
How to prove the cubic formula (from scratch)
I want to show you how to prove the arc length formula
Prove the summation formula: n(n+1)/2
How to Prove the Quadratic Formula - Just for fun! | Grade 9+ Series | GCSE Maths Tutor
06 - Proving the Logarithm (Log) Rules - Understand Logarithm Rules & Laws of Logs
Taylor series | Chapter 11, Essence of calculus
Proving an Integral Formula for the Beta Function
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
How to prove the formula of a curvature of a function (without using vector calculus)
Proving the Double and Half Angle Formulas for Trigonometry (Precalculus - Trigonometry 27)
How to Prove Trigonometric Identities (and how not to)
easy to state -- hard to prove
Integration by parts to prove the reduction formula (KristaKingMath)
Using mathematical induction to prove a formula
Комментарии
 0:06:16
0:06:16
 0:05:41
0:05:41
 0:07:08
0:07:08
 0:19:08
0:19:08
 0:00:36
0:00:36
 0:04:25
0:04:25
 0:08:51
0:08:51
 0:06:48
0:06:48
 0:04:53
0:04:53
 0:05:34
0:05:34
 0:40:16
0:40:16
 0:01:25
0:01:25
 0:07:40
0:07:40
 0:12:53
0:12:53
 0:16:39
0:16:39
 0:22:20
0:22:20
 0:06:49
0:06:49
 0:00:38
0:00:38
 0:09:37
0:09:37
 0:27:17
0:27:17
 0:07:37
0:07:37
 0:00:41
0:00:41
 0:07:28
0:07:28
 0:05:29
0:05:29