filmov
tv
Solving Math Equations but they keep getting HARDER | jensenmath.ca
Показать описание
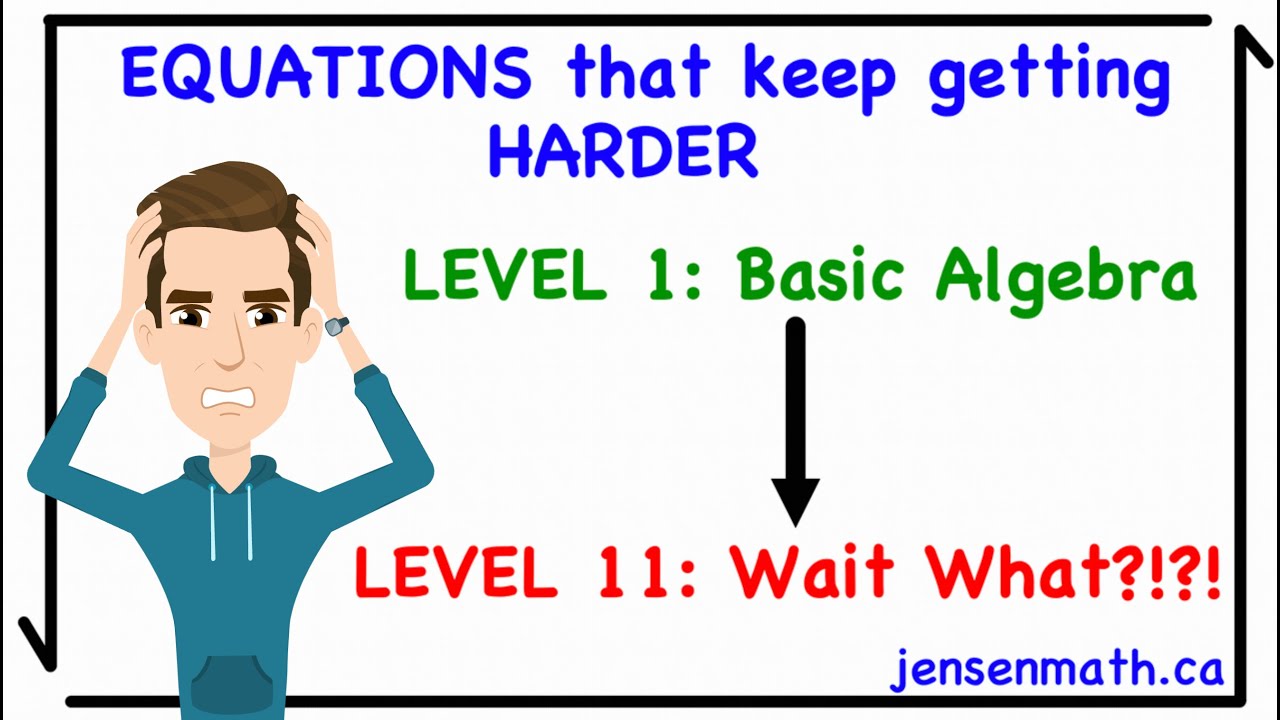
Welcome to JensenMath! In this video, we'll dive into 11 high school math equations, starting from fundamental algebraic expressions and progressing to more advanced topics like quadratic equations, exponentials, logarithms, and trigonometry. Whether you're a student looking to reinforce your understanding or a curious mind eager to explore the beauty of mathematics, this video is for you!
Throughout the video, we'll provide step-by-step explanations and examples to help you grasp each concept. Remember, math is not just about memorizing formulas; it's about understanding the underlying principles and applying them to solve problems.
0:00 - level 1 equation
1:06 - level 2 equation
2:22 - level 3 equation
3:33 - level 4 equation
5:14 - level 5 equation
6:08 - level 6 equation
8:33 - level 7 equation
10:55 - level 8 equation
13:57 - level 9 equation
16:43 - level 10 equation
20:55 - level 11 equation
Throughout the video, we'll provide step-by-step explanations and examples to help you grasp each concept. Remember, math is not just about memorizing formulas; it's about understanding the underlying principles and applying them to solve problems.
0:00 - level 1 equation
1:06 - level 2 equation
2:22 - level 3 equation
3:33 - level 4 equation
5:14 - level 5 equation
6:08 - level 6 equation
8:33 - level 7 equation
10:55 - level 8 equation
13:57 - level 9 equation
16:43 - level 10 equation
20:55 - level 11 equation
The Simplest Math Problem No One Can Solve - Collatz Conjecture
Learning Math
Stop Trying to Understand Math, Do THIS Instead
The 7 Levels of Math
Algebra Basics: Solving 2-Step Equations - Math Antics
Algebra Basics: Solving Basic Equations Part 1 - Math Antics
The Most Beautiful Equation in Math
Why You Can't Solve Every Equation (and Why That's Awesome)
Oxford University: Can you solve this Challenging Interview Test? #algebra
HOW COUNTRIES SOLVE MATH PROBLEMS #shorts
Algebra Basics: Solving Basic Equations Part 2 - Math Antics
270-year-old math problem SOLVED! Grazing goat problem
Anyone Can Be a Math Person Once They Know the Best Learning Techniques | Po-Shen Loh | Big Think
How to become a Math Genius.✔️ How do genius people See a math problem! by mathOgenius
Spain l can you solve this?? l Olympiad Math Exponential Problem
How to Solve One-Step Equations | One-Step Equation Steps | Math with Mr. J
9 Math Riddles That'll Stump Even Your Smartest Friends
Math Prof answers 6÷2(1+2) = ? once and for all ***Viral Math Problem***
Math Help : How to Solve Any Math Problem in Seconds
The Ultimate Problem–Solving Strategy | My Secret to Winning Physics, Math, and Coding Competitions...
The Hardest Math Test
Math isn't hard, it's a language | Randy Palisoc | TEDxManhattanBeach
How to Solve ANY Math Problem
The Algebra Word Problem That Stumps Everyone – Can You Solve It?
Комментарии
 0:22:09
0:22:09
 0:02:37
0:02:37
 0:05:21
0:05:21
 0:08:44
0:08:44
 0:10:29
0:10:29
 0:11:08
0:11:08
 0:03:50
0:03:50
 0:06:49
0:06:49
 0:11:59
0:11:59
 0:00:19
0:00:19
 0:09:35
0:09:35
 0:01:00
0:01:00
 0:03:53
0:03:53
 0:15:24
0:15:24
 0:11:56
0:11:56
 0:06:54
0:06:54
 0:06:40
0:06:40
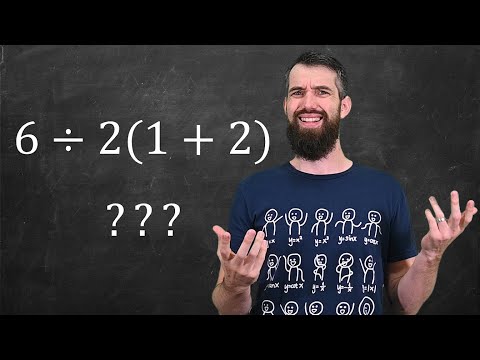 0:06:04
0:06:04
 0:01:15
0:01:15
 0:16:19
0:16:19
 0:00:28
0:00:28
 0:08:55
0:08:55
 0:05:43
0:05:43
 0:11:01
0:11:01