Monotone Sequence implies Least Upper Bound

Показать описание

Monotone Sequence Theorem implies Least Upper Bound Property

In this video, I prove a very interesting analysis result, namely that the Monotone Sequence Theorem is EQUIVALENT to the Least Upper Bound Property. This makes the least upper bound property more intuitive, in my opinion.

Dr Peyam

Рекомендации по теме

Комментарии

Loving the more analysis oriented video, thank you Dr. Peyam!

Was surprised completeness was never mentioned, this is like building the completeness of the real numbers right?

plaustrarius

I really like how a lot of famous theorems that follow from the least upper bound property actually turn out to be equivalent to it. Another simple example would be the intermediate value theorem – to see the reverse implication, given a nonempty set of real numbers S that is bounded above, just consider the set of upper bounds of S. If S did not have a least upper bound, the characteristic function of the set of upper bounds would be continuous everywhere in the real numbers whilst clearly violating the intermediate value theorem.

beatoriche

amazing. also I like failure reactions of Dr.

TheForever

Very cool proof. I find it a bit confusing to say we're working in R but we're not assuming the LUB property. I had to see the proof to figure out what we _are_ assuming besides monotone convergence, namely that we're working in an Archimedean ordered field.

We can also prove the Archimedean property if we want i.e. the sequence 1, 2, 3, ... is unbounded. Suppose there is an upper bound. Then the sequence converges by monotone convergence, let's say to L. But this is impossible since at most two terms of the sequence can be in the interval (L-1, L+1).

martinepstein

I think I've already asked it in another video, but did you make a video on the proof of the LUB, just based on the definition (or construction of) R?

jonasdaverio

How is 2^(-M) a big number? Shouldn't it be a really small number?

toaj

I search for monotone types in CSS and this showsup.

Myrslokstok

Monotone Sequence implies Least Upper Bound

Monotone Sequence implies Least Upper Bound

Monotonic Sequences and Bounded Sequences - Calculus 2

Lecture 20(B): Bounded Sequences: The Monotone Convergence Theorem

Connections Between Supremums and Infimums and Limits of Monotone Sequences [Real Analysis]

least upper bound of the bounded sequence Monotonic real analysis iit jam 2016 mathematics solution

Proof of the Monotone Convergence Theorem (ILIEKMATHPHYSICS)

Detailed Proof of the Monotone Convergence Theorem | Real Analysis

Monotonic Sequence #realanalysis

Riemann Integrability of Monotonic Functions (Part 2, Tao)

Monotone Sequence Theorem

Bounded, monotone sequences.

Monotone Convergence Theorem

023 Monotonic Sequences I

Monotonic Sequences and Subsequences.

Prove MCT monotone convergence theorem

Real Analysis | The monotone sequence theorem.

Monotone Sequences Definition, Monotone Increasing and Decreasing Examples [Real Analysis]

Monotone Convergence Theorem Easiest Proof

|Infinite Series| Convergence And Divergence Of Monotonic Sequences |Formula Foundation|

Sequences (Theorem on monotonic sequences)

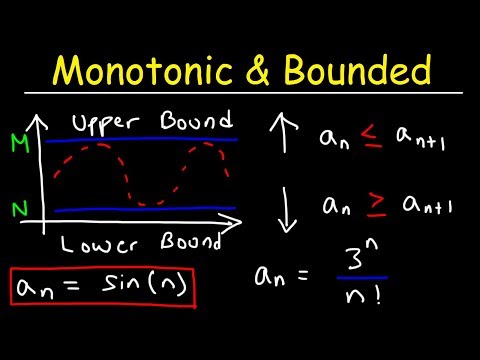
Monotonic & Bounded Sequences

A Bounded Monotonic Sequence is Convergent Proof (Real Analysis Course #20)

Logic - Bounded Monotonic Sequence Convergence Theorem

(RA07) Monotonicity of Sequences