A Bounded Monotonic Sequence is Convergent Proof (Real Analysis Course #20)

Показать описание

Here we will prove that a bounded monotonic sequence is convergent. This is a great proof taking advantage of the supremum and giving us a quite a famous result! Enjoy.

#realanalysis #brithemathguy #math

🙏Support me by becoming a channel member!

Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.

Рекомендации по теме

Комментарии

🎓Become a Math Master With My Intro To Proofs Course! (FREE ON YOUTUBE)

BriTheMathGuy

I'm really impressed with the speed he writes a reflected version of those sentences

ismailsheik

It's been a while, I'm glad you're back.

usernamehere

We need you to continue Real analysis tutorial. Thank you

asmrEveryday

It is awesome to see you back as well. I'm actually in my first year as a mathematics student and your vids have been an awesome source of learning for me. thanks!

canadianmaple

This playlist is a gem, please make more videos! Thank you

hannananan

please continue this real analysis series!

axog

Can you please make videos on the "tests" and their proofs in real analysis? Like the limit test, root test, comparison test, etc...

mathgeek

Sorry, isn't there a small typo in the proof? It does not change the result but still: last line, second to last inequality should not be strict as you imposed that the sequence is not strictly monotonic (in the line above the inequality is not strict).

danilolewanski

I have had the idea to do this kind of series for analysis. Short videos of the most important proofs. Thanks man.

Mr_mechEngineer

Nice video! I think by bounded, you need |a_n| \leq B because the secquence a_n = - n is not bounded but has the property a_n \leq B for some B.

Also, I dont understand why there is an if and only if. You only proved the if part, but the only if is not true I guess. Not every convergent sequence is monotonic and bounded. Take for example a_n = (-1)^n /n. It is a convergent sequence to 0, bounded, but not monotonic.

Keep up the good work, love your vids! 😊

bramlentjes

You said Am is less than a - epsilon but wrote Am > a - epsilon.

kaisiasima

your face is kinda distracting i was watching you the whole time

meenugoyal-csjr

A Bounded Monotonic Sequence is Convergent Proof (Real Analysis Course #20)

Monotonic Sequences and Bounded Sequences - Calculus 2

Intro to Monotonic and Bounded Sequences, Ex 1

Monotonic and bounded sequences

A Bounded Monotonic Sequence is Convergent Proof (Real Analysis Course #20)

How to Determine if a Sequence is Monotonic and Bounded: Example with n/(n^2 + 1)

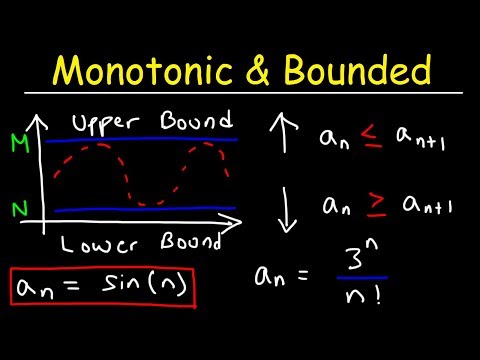
Monotonic & Bounded Sequences

What are Monotone Sequences? | Real Analysis

9.1 Supplement - Monotonic and Bounded Sequences

Riemann Integrability of Monotonic Functions (Part 2, Tao)

Monotonic and Bounded Sequences | Calculus 2 | Math with Professor V

Detailed Proof of the Monotone Convergence Theorem | Real Analysis

How to Determine if a Sequence is Bounded using the Definition: Example with a_n = 1/(2n + 3)

Bounded, monotone sequences.

THS 9 1 6 Bounded Monotonic Sequences

Bounded and Monotonic Sequences

Monotonic Sequence Theorem - Full Example Explained

A Bounded Monotonic Sequence is Convergent Real Analysis in English

Ex 1: Determine if a Sequence in the Form (a^n/b^n) is Bounded, Monotonic,and Convergent

Unit 3 Video 5 Monotonic and Bounded Sequences

Monotonic & Bounded Sequences | Calculus 2 Lesson 19 - JK Math

Ch 9-1 Monotonic and Bounded Sequences (Ex 8-9)

11.4 Monotonic and bounded sequences

monotonic Sequences full definition and example most IIT JAM

Calculus II - 9.1.3 Monotonic and Bounded Sequences