filmov
tv
Monotone Sequence Theorem

Показать описание
Monotone Sequence Theorem
In this video, I prove the celebrated Monotone Sequence Theorem, which says that an increasing sequence that is bounded above must converge. This is the fundamental theorem of sequences, because it allows us to easily prove convergence of sequences
In this video, I prove the celebrated Monotone Sequence Theorem, which says that an increasing sequence that is bounded above must converge. This is the fundamental theorem of sequences, because it allows us to easily prove convergence of sequences
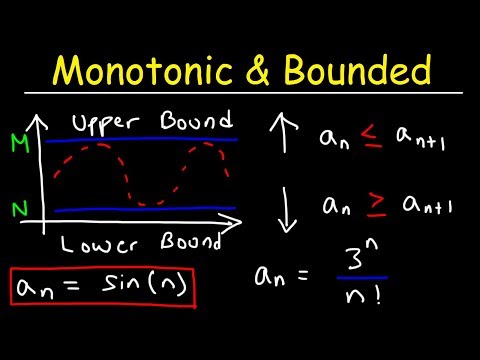
Monotonic Sequences and Bounded Sequences - Calculus 2
What are Monotone Sequences? | Real Analysis
Detailed Proof of the Monotone Convergence Theorem | Real Analysis
Real Analysis | The monotone sequence theorem.
Monotone Sequence Theorem
How to prove monotone sequences
Monotone Sequence Theorem
Sequences (Theorem on monotonic sequences)
Real Analysis | Monotone sequence theorem example.
How to Determine if a Sequence is Monotonic and Bounded: Example with n/(n^2 + 1)
Monotone Convergence Theorem for Sequences
Bounded, monotone sequences.
Bounded and Monotonic Sequences
Monotone Sequences
Monotonic and Bounded Sequences | Calculus 2 | Math with Professor V
Using the Monotone Convergence Theorem! | Real Analysis
A Monotonic Sequence is convergent iff it is Bounded | Monotone convergence theorem | Real Analysis
Monotonic Sequence Theorem - Full Example Explained
Intro to Monotonic and Bounded Sequences, Ex 1
Monotone Convergence Theorem
A Bounded Monotonic Sequence is Convergent Proof (Real Analysis Course #20)
Calculus I: Monotonic Sequences and the Monotone Sequence Theorem
401.6 Using Monotone Convergence
Monotone sequence
Комментарии
 0:31:23
0:31:23
 0:12:41
0:12:41
 0:13:44
0:13:44
 0:09:17
0:09:17
 0:18:55
0:18:55
 0:15:29
0:15:29
 0:19:05
0:19:05
 0:10:16
0:10:16
 0:08:46
0:08:46
 0:08:02
0:08:02
 0:06:38
0:06:38
 0:27:28
0:27:28
 0:04:46
0:04:46
 0:00:50
0:00:50
 0:41:57
0:41:57
 0:05:50
0:05:50
 0:19:49
0:19:49
 0:04:54
0:04:54
 0:03:42
0:03:42
 0:08:55
0:08:55
 0:04:01
0:04:01
 0:08:21
0:08:21
 0:11:54
0:11:54
 0:15:45
0:15:45