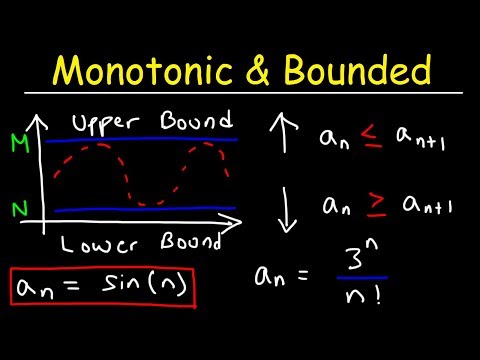
Bounded, monotone sequences.

Показать описание

An introduction to the convergence property of monotonic and bounded sequences. The main idea is known as the "Monotonic convergence thoerem" and has important applications to approximating solutions to equations. Several examples are presented to illustrate the ideas.

Рекомендации по теме

Комментарии

Thank you kind sir! I am an external student from another Australian University, I cannot tell you how much visual lectures aid the student. Bravo!

tgc

Sir, please develop a lecture series on "Elementary to Advanced Real Analysis" so that people like me can understand horrific Walter Rudin's proofs easily.

bitsntube

All convergent sequences are bounded but not all bounded sequences are convergent.

A different example: (-1)^n.
This just alternates from -1 and 1 thus is bounded (by -1 and 1). However this does not converge.

So we found a bounded sequence which does NOT converge.
I guess the theorem only works one way.
All sequences that converge must also be bounded. But not all sequences that are bounded necessarily converge.

Rabixter

Good luck with your studies and thanks for the feedback.

DrChrisTisdell

Hi - your sequence is bounded (above and below) for all n \ge 1, which is the range of n values that we are interested in. Actually, we are really only interested in values of n large and positive.

DrChrisTisdell

Thanks you a lot Dr. Exam tomorrow. At least now I can find a way out..

chesterbennin

Your are one of the best YT-teachers! And I've seen them all, so a better review than that is hard to get.

A question though. (I was listening to your video while cooking so apologize if I missed something). Why didn't you use the term "supremum" for the least upper bound?
Did you want to stay clear of any new definitions that could confuse your class?
IMO the definition "supremum" is quite nice to have, mostly because you can in short write something like "sup M" for the supremum of a set M. Or i guess "LUB M" would do just a fine =)
I know the terminology doesn't matter much, but it makes me wonder if this quote from wikipedia is one reason: "the monotone convergence theorem is any of a number of related theorems proving the convergence of monotonic sequences".

Could it be so that you skipped introducing supremum so that you didn't have to go into one of these other theorems wikipedia mentions?

sunnyhours

The theorem states that all bounded monotonic sequences converge. Since (-1) ^ n is not monotonic, you cannot use the MCT with it.

StevePurol

Hi Dr i have a question you can solve it

AMath-ujlr

Sir can i know what is that book which you are referring in this video

wishwagayan

Bounded, monotone sequences.

Monotonic Sequences and Bounded Sequences - Calculus 2

What are Monotone Sequences? | Real Analysis

Bounded, monotone sequences.

How to Determine if a Sequence is Monotonic and Bounded: Example with n/(n^2 + 1)

Monotonic and bounded sequences

Monotonic and Bounded Sequences | Calculus 2 | Math with Professor V

Intro to Monotonic and Bounded Sequences, Ex 1

How to prove monotone sequences

Example of Using the Monotonic Sequence Theorem | Calculus 2

Calculus II - 9.1.3 Monotonic and Bounded Sequences

Detailed Proof of the Monotone Convergence Theorem | Real Analysis

Bounded sequences (KristaKingMath)

Real Analysis | The monotone sequence theorem.

Determine if sequence is increasing or decreasing, not monotonic, bounded {(2n-3)/(3n +4)}

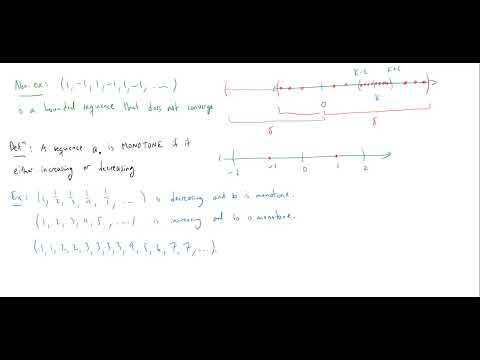
Bounded and Monotone Sequences

Monotonic Sequence, Eventually Monotonic Sequence with examples | Sequence of real numbers : 02

How to Determine if a Sequence is Bounded using the Definition: Example with a_n = 1/(2n + 3)

Monotonicity And Boundedness

10 1 Monotone sequences

Calculus II, Lecture 20, V8 Bounded Monotone Sequences

Real Analysis | Monotonic Sequence - Bounded Sequence | Definition & Examples

Sequences - Increasing, decreasing, bounded and monotonic sequences

Bounded and Monotone sequence

Every monotone decreasing sequence converges to infimum if it is bounded