filmov
tv
Example of Radioactive Decay 1

Показать описание
Calculus/ODEs: Carbon-14 has a half-life of 5,715 years. A fossil has lost 75% of its original amount of C-14. How old is the fossil? How much C-14 remains after 50,000 years?
Example of Radioactive Decay 1
GCSE Physics - Radioactive Decay and Half Life #35
Calculation of the radioactive decay
Radioactive Decay Half Life Example
Radioactive Decay (Example 1)
Differential Equations: Radioactive Decay: Example 1
Half life | Radioactivity | Physics | FuseSchool
What is Radioactive Decay? Half Life | Decay Constant | Activity (+ Problems Solving)
Nuclear Medicine Physics Questions and answers Part 1
Radioactive Decay and Exponential Growth: Quick Example Involving Exponential Decay
Radioactivity (8 of 16) Decay Activity, An Explanation
Example of Radioactive Decay 2
What is Radioactivity and Is It Always Harmful: Explained in Really Simple Words
How Radioactive Decay Works? Explained With Animation
Half Life Chemistry Problems - Nuclear Radioactive Decay Calculations Practice Examples
Intro to radioactive decay | Physics | Khan Academy
Radioactivity (10 of 16) Decay Activity, Example Problems
Radioactive decay example 1
Radioactivity (11 of 16) Radioactive Decay Law, An Explanation
Exponential Decay: Half Life
Simulating Radioactive Decay With Dice - Physics Experiment
Find Age of Substance From Given Half Life Exponential Decay
Radioactive Decay Exponential Part 1
Half-Life and Radioactive Decay
Комментарии
 0:05:03
0:05:03
 0:06:27
0:06:27
 0:02:45
0:02:45
 0:04:53
0:04:53
 0:03:39
0:03:39
 0:24:19
0:24:19
 0:04:54
0:04:54
 0:23:28
0:23:28
 0:28:03
0:28:03
 0:02:17
0:02:17
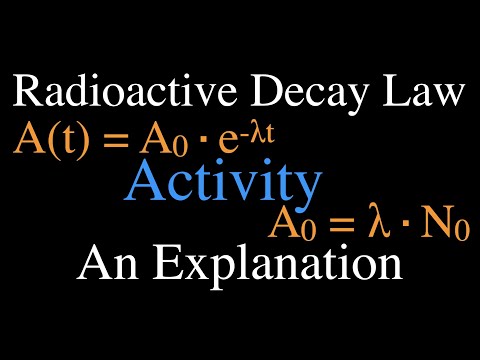 0:11:07
0:11:07
 0:07:23
0:07:23
 0:08:08
0:08:08
 0:00:59
0:00:59
 0:08:10
0:08:10
 0:08:02
0:08:02
 0:13:24
0:13:24
 0:07:44
0:07:44
 0:10:36
0:10:36
 0:04:46
0:04:46
 0:02:20
0:02:20
 0:03:31
0:03:31
 0:09:41
0:09:41
 0:07:42
0:07:42