filmov
tv
Direct Image of Intersection of Sets under an Injective Function Proof

Показать описание
Direct Image of Intersection of Sets under an Injective Function Proof. Give an injective function f from X to Y and two subsets A, B of X, this video proves that the direct image of the intersection is the intersection of the direct images; i.e., f(A n B) = f(A) n f(B).
Direct Image of Intersection of Sets under an Injective Function Proof
Preimage(Inverse Image) Explanation and Intersection of Sets Proof
Inverse Image(Preimage) of Intersection of Sets Proof
Questions from the Hardest Math Textbooks - Image of Intersections is an Intersection of Images
Image of intersection of two sets intersection of images.
How REAL Men Integrate Functions
Finding the solution set of union and intersection
Intersection of Equivalence Relations
Design of Holographic Display Systems based on Artificial Intelligence
Ambush at intersection near Sderot during Hamas attack in Israel | Traffic cam video
Inverse of union and intersection of sets
Proof with Sets Example with Intersection and Union
inverse image of intersection of two sets # real analysis # TAM5B # Explained in Tamil
Looking at a REAL Human Tongue
The Inverse Image of a Set Under a Function: Definition and Examples
Operations on Sets : Intersection of Sets (in English) & its Venn Diagram for Class 11 Maths
Finite intersection property| The image of a compact space under a continuous map is compact
Operations on Sets : Intersection of Sets & its Venn Diagram for Class 11 Maths : Basic Concepts
Excel INDIRECT Function: Lookup Values in Different Sheets / Excel Tabs
Unions of Sets, Intersection of Sets [Real Analysis]
base de l'intersection de 2 sous-espaces vectoriels E∩F • Exercice • prépa MPSI PCSI ECS
53 Distributive Law for Union over Intersection proof using Venn Diagra
Unique Method to Quickly Trim All Intersections in AutoCAD
Understanding the mAP (mean Average Precision) Evaluation Metric for Object Detection
Комментарии
 0:06:21
0:06:21
 0:03:56
0:03:56
 0:05:39
0:05:39
 0:03:09
0:03:09
 0:33:13
0:33:13
 0:00:35
0:00:35
 0:04:13
0:04:13
 0:04:42
0:04:42
 1:15:37
1:15:37
 0:00:52
0:00:52
 0:10:23
0:10:23
 0:02:36
0:02:36
 0:03:31
0:03:31
 0:00:39
0:00:39
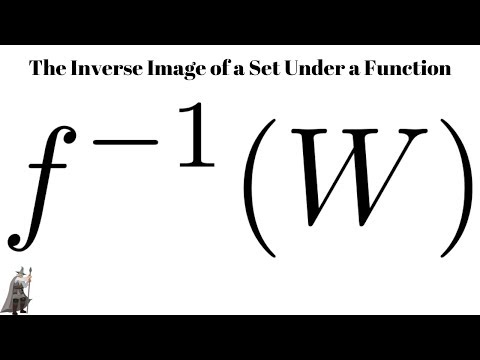 0:06:52
0:06:52
 0:09:20
0:09:20
 0:28:23
0:28:23
 0:08:17
0:08:17
 0:11:40
0:11:40
 0:07:35
0:07:35
 0:05:13
0:05:13
 0:04:14
0:04:14
 0:00:58
0:00:58
 0:18:24
0:18:24