filmov
tv
Deriving the formula for angle between two straight lines

Показать описание
In this video , I showed how to obtain the formula for the angle between two lines using the slopes
Angle Sum Formula Proof with Linear Algebra!
Compound Angle Formula Proof
Proof of angle addition formula for sine | Trigonometry | Khan Academy
The Double-Angle Formulas | proof without words| mathocube|
Compound Angle Identities (1 of 3: Proving sin(a+b) geometrically)
deriving the double angle formulas
Angle Between Two Lines (Derivation)
Derive Formula for Angle Between Clock Hands and Find Time for Given Situation in Seconds
Right Angle Triangle | SAT Geometry
Half Angle Tangent Formulas (visual proof; trigonometry)
A-Level Maths: E6-01 Compound Angles: Proving the Compound Angle Formulae
Proving the Formula for the Angle Between Two Vectors
Solid Angle Derivation & Intuition
Verifying Trigonometric Identities With Double Angle Formulas
How do you find the angle? Let’s see…
Proving the Double and Half Angle Formulas for Trigonometry (Precalculus - Trigonometry 27)
A-Level Maths: E6-04 Compound Angles: Introducing the Double Angle Formulae
How To Calculate The Missing Angle In a Triangle
Double Angle Identities & Formulas of Sin, Cos & Tan - Trigonometry
Trigonometry - Proof of the Double Angle Formulae : ExamSolutions
A-Level Maths E2-01 Small-Angle Approximation: Geometrical Derivation
Half Angle Formulas & Identities - Evaluating Trigonometric Expressions
Finding Angle Between 2 Lines (Formula)
GCSE Maths - Alternate, Corresponding and Allied Angles - Parallel Lines Angle Rules #117
Комментарии
 0:01:59
0:01:59
 0:07:24
0:07:24
 0:08:26
0:08:26
 0:02:36
0:02:36
 0:13:19
0:13:19
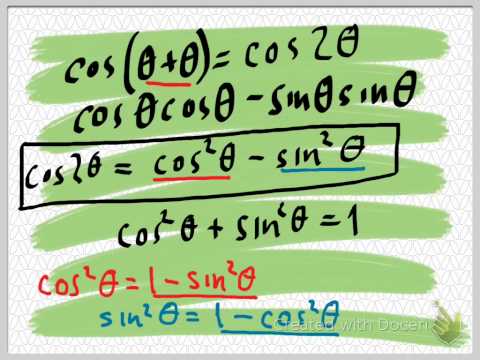 0:07:49
0:07:49
 0:10:01
0:10:01
 0:13:37
0:13:37
 0:00:46
0:00:46
 0:02:11
0:02:11
 0:14:39
0:14:39
 0:06:16
0:06:16
 0:07:19
0:07:19
 0:15:19
0:15:19
 0:15:46
0:15:46
 0:27:17
0:27:17
 0:04:11
0:04:11
 0:14:33
0:14:33
 0:18:16
0:18:16
 0:08:25
0:08:25
 0:08:43
0:08:43
 0:10:15
0:10:15
 0:01:29
0:01:29
 0:05:36
0:05:36