filmov
tv
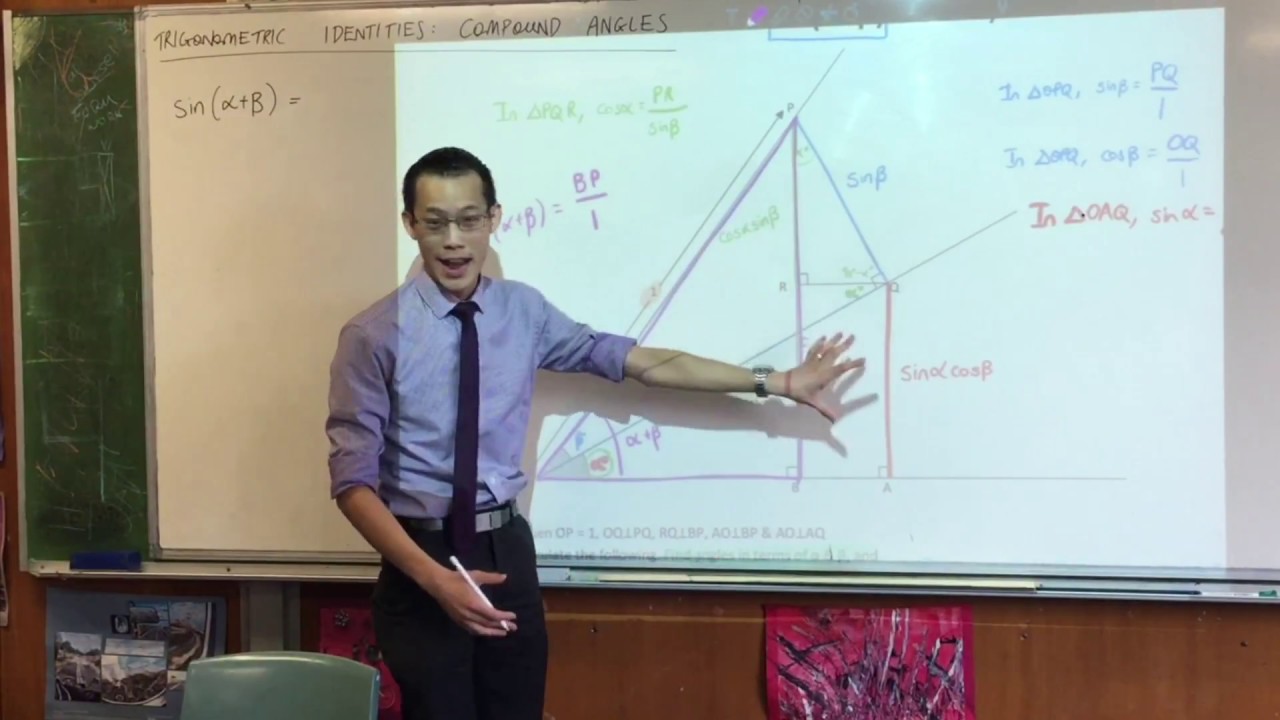
Compound Angle Identities (1 of 3: Proving sin(a+b) geometrically)
Показать описание
Compound Angle Identities (1 of 3: Proving sin(a+b) geometrically)
Compound Angle Identities (1 of 4: Sine)
Trigonometric Identities with Compound Angle Formula Part 1
Trigonometric Equation with Compound Angle (1 of 2: Using identities)
Compound Angle Formula Part 1
TRIGONOMETRY-COMPOUND ANGLE IDENTITIES-GRADE 12 Lesson 1
AS/A-Level Maths Trigonometry - Compound angle transform PART 1
AS/A-Level Maths Trigonometry - Compound angle identities
DMT and Trig Identities (1 of 4: Deriving multi-angle identities with compound angles)
Trigonometry: Compound Angles - A-Level Maths
Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)
Trigonometry - how to use the compound angle formulae to solve equations
Prove Trigonometric Identity Using Compound Angle Formula
Compound Angle formulas [ Trigonometric Identities, Part 1 ]
Compound Angle Formula For Trigonometric Identities
Compound Angle Formula Proof
Grade 12 Trig - Topic 1 - Compound Angle Identities
Trigonometry Compound Angle Formula Applications MHF4U
New 2024 | Compound Angles Grade 12
OCR MEI Core 4 1.17a Using the Compound Angle Formulas: Finding the exact value of sin 105
Trig Identities
Simplify Ratio of Sum of Sine and Cosine Compound Angle Formula Trigonometry
Compound Angle Formula Part 2
Proof of Compound Angle Identities
Комментарии
 0:13:19
0:13:19
 0:17:33
0:17:33
 0:13:58
0:13:58
 0:12:58
0:12:58
 0:09:54
0:09:54
 0:17:35
0:17:35
 0:25:59
0:25:59
 0:28:01
0:28:01
 0:08:31
0:08:31
 0:18:00
0:18:00
 0:04:15
0:04:15
 0:03:42
0:03:42
 0:03:17
0:03:17
 0:02:21
0:02:21
 0:07:50
0:07:50
 0:07:24
0:07:24
 0:30:13
0:30:13
 0:22:42
0:22:42
 0:18:47
0:18:47
 0:06:15
0:06:15
 0:27:57
0:27:57
 0:04:42
0:04:42
 0:09:58
0:09:58
 0:18:28
0:18:28