filmov
tv
How to prove monotone sequences

Показать описание
in this video I used Bernoulli's inequality to show that a sequence in monotonic increasing. I took this approach because not all classes allow the use of derivatives to show that a sequence in monotone
How to prove monotone sequences
Monotonic Sequences and Bounded Sequences - Calculus 2
What are Monotone Sequences? | Real Analysis
Detailed Proof of the Monotone Convergence Theorem | Real Analysis
401.6 Using Monotone Convergence
Monotonic Sequences - Increasing Decreasing Sequences
Using the Monotone Convergence Theorem to Prove a Recursive Sequence Converges: Example 1
Real Analysis | Monotone sequence theorem example.
Monotone Convergence Theorem for Sequences
Real Analysis | The monotone sequence theorem.
Monotonic Sequence, Eventually Monotonic Sequence with examples | Sequence of real numbers : 02
Monotone Sequence Theorem
Showing that a sequence is monotone increasing and bounded
Using the Monotone Convergence Theorem! | Real Analysis
Using the Monotone Convergence Theorem to Prove a Recursive Sequence Converges: Example 2
Sequences 4 - Example of Monotone Convergence Theorem
Monotone Sequence | Monotonically increasing | Monotonically decreasing | Definition | Examples
How can the Monotone Convergence Theorem help? - Week 1 - Lecture 15 - Sequences and Series
10 1 Monotone sequences
Proof: Monotone Sequence has Monotone Subsequences | Real Analysis
Monotone sequence
Real Analysis | Monotonic Sequence - Bounded Sequence | Definition & Examples
11.6 The monotone convergence theorem for sequences
Monotone Sequences
Комментарии
 0:15:29
0:15:29
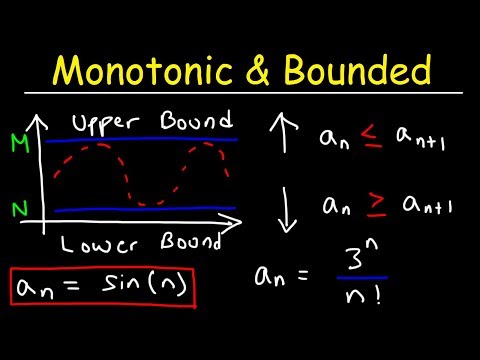 0:31:23
0:31:23
 0:12:41
0:12:41
 0:13:44
0:13:44
 0:11:54
0:11:54
 0:05:57
0:05:57
 0:04:54
0:04:54
 0:08:46
0:08:46
 0:06:38
0:06:38
 0:09:17
0:09:17
 0:36:03
0:36:03
 0:19:05
0:19:05
 0:13:14
0:13:14
 0:05:50
0:05:50
 0:05:00
0:05:00
 0:05:15
0:05:15
 0:10:54
0:10:54
 0:05:45
0:05:45
 0:11:40
0:11:40
 0:06:10
0:06:10
 0:15:45
0:15:45
 0:13:26
0:13:26
 0:07:47
0:07:47
 0:00:50
0:00:50