filmov
tv
Area of Circles Inscribed in Squares | Geometry, Inscribed Circles, Finding Area

Показать описание
How do we find the area of a circle inscribed in a square? How do we find the area of the square? What about the region in the square but outside of the inscribed circle? We go over all of those area calculation in today's math lesson!
A circle inscribed in a square is a circle that is tangent to all four sides of the square, which means each side of the square intersects the circle exactly once. A circle inscribed in a square has a diameter length equal to the side length of the square, which allows us to find all the areas we need. Watch the video lesson for a more detailed walkthrough!
Here is the answer to the question posed at the end of the video. The area of the region in the square but not in the circle is the area of the square minus the area of the circle, which is 64 cm^2 - 16*pi cm^2, which is approximately 13.7 cm^2.
I hope you find this video helpful, and be sure to ask any questions down in the comments!
********************************************************************
The outro music is by a favorite musician of mine named Vallow, who, upon my request, kindly gave me permission to use his music in my outros. I usually put my own music in the outros, but I love Vallow's music, and wanted to share it with those of you watching. Please check out all of his wonderful work.
********************************************************************
+WRATH OF MATH+
Follow Wrath of Math on...
A circle inscribed in a square is a circle that is tangent to all four sides of the square, which means each side of the square intersects the circle exactly once. A circle inscribed in a square has a diameter length equal to the side length of the square, which allows us to find all the areas we need. Watch the video lesson for a more detailed walkthrough!
Here is the answer to the question posed at the end of the video. The area of the region in the square but not in the circle is the area of the square minus the area of the circle, which is 64 cm^2 - 16*pi cm^2, which is approximately 13.7 cm^2.
I hope you find this video helpful, and be sure to ask any questions down in the comments!
********************************************************************
The outro music is by a favorite musician of mine named Vallow, who, upon my request, kindly gave me permission to use his music in my outros. I usually put my own music in the outros, but I love Vallow's music, and wanted to share it with those of you watching. Please check out all of his wonderful work.
********************************************************************
+WRATH OF MATH+
Follow Wrath of Math on...
Комментарии
 0:07:41
0:07:41
 0:11:39
0:11:39
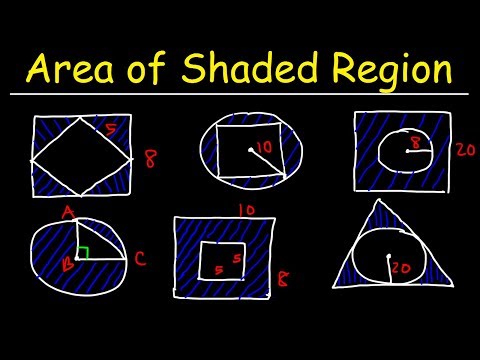 0:13:36
0:13:36
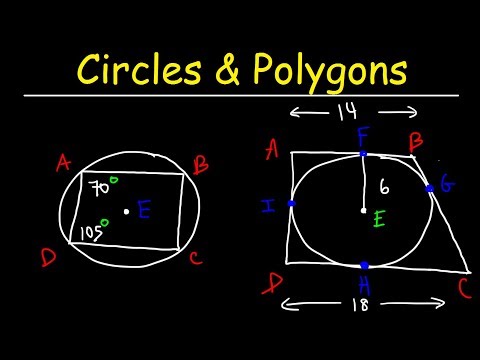 0:12:50
0:12:50
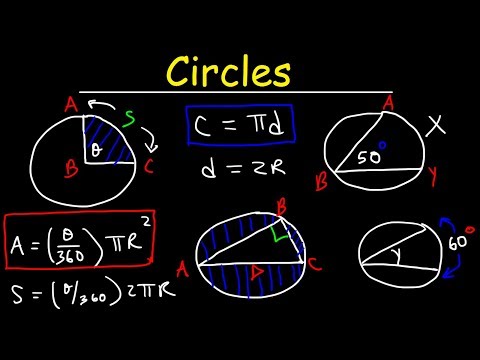 0:18:07
0:18:07
 0:03:35
0:03:35
 0:05:00
0:05:00
 0:03:58
0:03:58
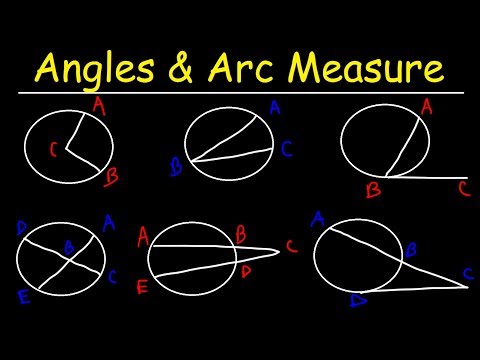 0:32:31
0:32:31
 0:00:44
0:00:44
 0:04:31
0:04:31
 0:05:35
0:05:35
 0:04:09
0:04:09
 0:06:06
0:06:06
 0:23:35
0:23:35
 0:11:58
0:11:58
 0:05:58
0:05:58
 0:17:05
0:17:05
 0:09:40
0:09:40
 0:01:46
0:01:46
 0:05:32
0:05:32
 0:16:18
0:16:18
 0:03:02
0:03:02
 0:17:20
0:17:20