Inscribed Polygons and Circumscribed Polygons, Circles - Geometry

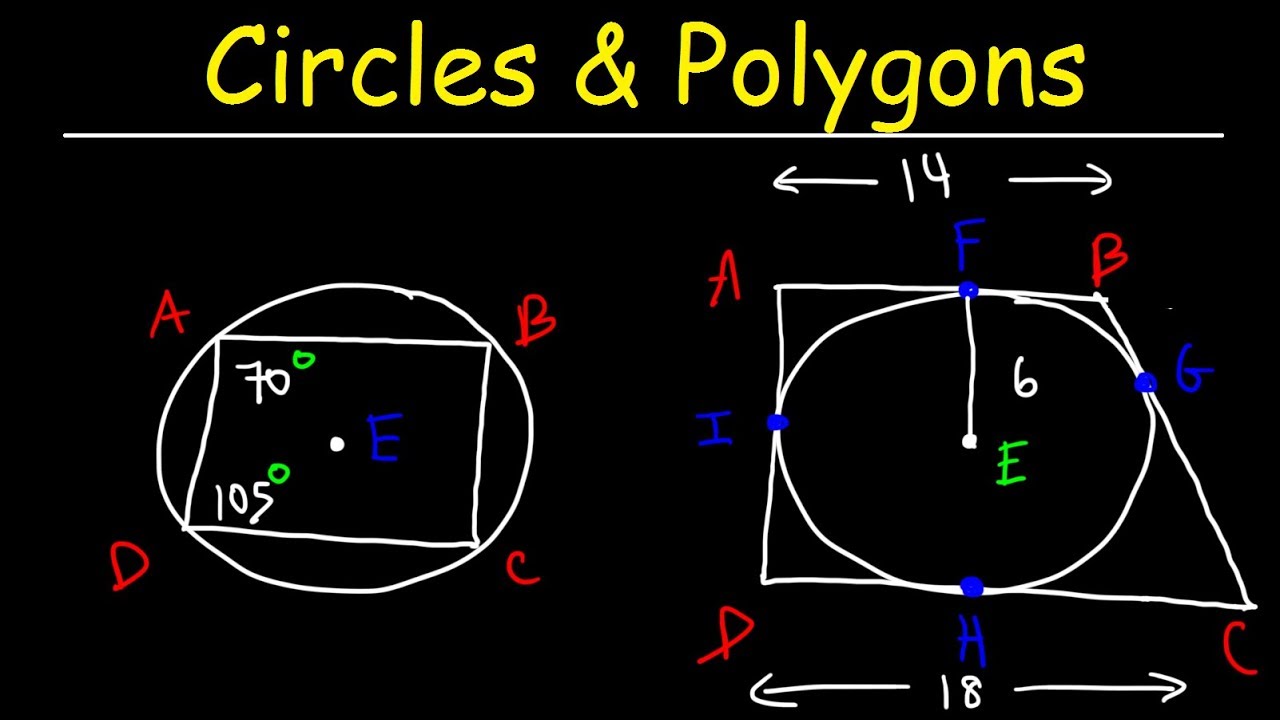
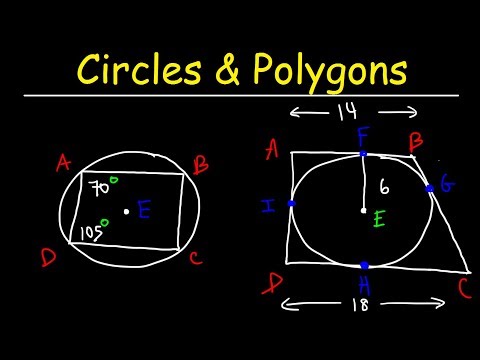
This geometry video tutorial provides a basic review into inscribed polygons and circumscribed polygons with reference to circles. The opposite angles of a quadrilateral inscribed in a circle are supplementary. This video also explains how to solve the walk around problem when a circle is inscribed in a quadrilateral or when a quadrilateral is circumscribed about a circle. The incenter is the center of the circle when a circle is inscribed in a polygon. The circumcenter is the center of the circle when the circle is circumscribed about the polygon. This geometry video tutorial contains plenty of examples and practice problems.

Circles - Area, Circumference, Radius:

Circles - Chords, Radius, & Diameter:

Lines, Rays, Line Segments, & Angles:

2 Column Proofs - Cong. Segments:

Triangle Congruence - SSS, SAS, ASA:

Central Angles and Circle Arcs:

___________________________________
Tangent Lines and Secant Lines:

Circles - Central and Inscribed Angles:

Tangent Tangent Angle Theorems:

Power Theorems - Chords, Secants, & Tangents:

Circle Theorems:

_________________________________
Two Column Proofs With Circles:

Circles Review - Geometry:

Incenter, Circumcenter, and Orthocenter:

Distance Between Point and Line in 2D & 3D:

Area of a Triangle With Vertices:

________________________________
Coordinate Geometry:

Geometry Review - Study Guide:

Geometry Final Exam Review:

Final Exams and Video Playlists:

Full-Length Videos and Worksheets:

[slushii]

I hate geometry but this guy makes it bearable

[paulwittekind]

Hey
Thank You
For
Every video.
I like you. Somehow we need more people like you in our country.

[gcmrgcmr]

i need to do binge watch of all his math videos just to understand the whole quarter of math subj bcs i didn't learn so well...ty so much

[thanosmishra]

No matter what topic of mathematics i search, this channel videos always appear on top 🔥🔥🔥

[originalname]

I’m here because I have a geometry test and my teacher never taught us this

[georgesadler]

MR. Organic Chemistry Tutor, thank you for another well explained video/lecture on Inscribed Polygons, Circumscribed Polygons and Circles in Solid Geometry. There is a pattern when solving these types of problems in Geometry from start to finish.

[namankhandelwal]

In the last problem, use the property : sum of opposite sides of a quadrilateral are equal if a circle is inscribing it.
∴ (AB + DC) = (AD + BC)
⇒ 14 + 18 = 12 + x gives x = 20

[dagmwitmelkamu]

it is absolutely helpful i have test tomorrow and you saved my life

[sajeevmagesh]

on the last question the answer is 44+4sqrt(10), because if you drop the altitude of the trapezoid you get the altitude to be 12. using the pythagorean theorem you get 12^2 + 4^2 = BC^2, 160=BC^2, BC= 4sqrt(10). find perimeter and you get 44+4sqrt(10)

[Aprendiz-xszb]

En 8:00... ejemplo 2, si aplicamos el Teorema de Pitot, tenemos AB+DC=AD+BC. Si AB+DC=14+18=32, entonces AD+BC también suman 32; por tanto, 32+32=64. Ese es el perímetro. (At 8:00... example 2, if we apply Pitot's Theorem, we have AB+DC=AD+BC. If AB+DC=14+18=32, then AD+BC also add up to 32; therefore, 32+32=64. That's the perimeter)

[jude]

This video is helpful...hope you upload more...thanks

[moshegoodman]

You made a mistake on the video
A trapeze as you described cannot have a circle inscribed that would touch all four sides
The length of bc is 4^2+12^2=bc^2
BC=√160

[crazyjester]

9:05 two tangent theorem - two tangent start from one exterior point.
x and y their summation x+y=14

[ragedragon]

Iam here because my mom wanted me to study this ;-;

[sopcntuli]

AD can only be 12 if Angle A and Angle B are right angles, I missed that part if it is mentioned anywhere

[lizettelucas]

When you have to watch yt videos because your teacher never taught you this.

[cpSweatyFC]

Could the last problem be solved using the Pythagorean theorem?

[MosMoses-ht]

5:30 is this bell 🔔 I think he recorded this video in the last period however thanks for doing 3asy😂😂

[a.b]

I hate geometry. This is the worst thing ever.

[azharaitkali]

Reply to this comment only after 1 year