filmov
tv
Differential Equations - 16 - Exact with Integrating Factor EXAMPLE

Показать описание
Example, demonstrating how to solve a non exact differential equation using an integrating factor
Solving Linear Differential Equations with an Integrating Factor (Differential Equations 16)
Differential Equations - 16 - Exact with Integrating Factor EXAMPLE
🔵16 - Bernoulli Differential Equations (dy/dx + p(x)y = q(x)y^n)
2016 SQA Advanced Higher Mathematics No. 16 Differential Equation Model
Differential Equation - Introduction (2 of 16) Real Situations Represented in Differential Equations
Differential Equation - Introduction (1 of 16) What is a Differential Equation?
Differential Equation - Introduction (14 of 16) Second Order Differential Eqn. Linear vs Non-Linear
NBHM 2024 Q16 Solution | Maximum and Minimum Modulus Principal | Complex Analysis
Differential Equation - Introduction (16 of 16) 2nd Order Differential Eqn. Linear Non-Homogeneous
Solutions of Nonhomogeneous Equations - Ordinary Differential Equations | Lecture 16
[Numerical Modeling 16] Iterative solution of differential equations using finite difference method
How to determine the general solution to a differential equation
Differential Equation - Introduction (15 of 16) Second Order Differential Eqn. Linear Homogeneous
Electrical Engineering: Ch 16: Laplace Transform (30 of 58) Solving Differential Equation Ex. 1
Differential Eqns. F22-16 -- Elimination method for systems of equations (BONUS)
12.1: Separable Partial Differential Equations
Solve the Fourth Order Differential Equation d^4y/dx^4 - 8d^2y/dx^2 + 16y = 0
Differential Equations Practice #16: (x - 2y)dx + (2x + y)dy = 0
🔵03 - Linear and Non-Linear Differential Equations: Solved Examples
Case 2: complex-conjugate roots (Part B) | Lecture 16 | Differential Equations for Engineers
Electrical Engineering: Ch 16: Laplace Transform (32 of 58) Solving Differential Equation Ex. 3
Differential Equations Book for Beginners
Differential Equations || Lec 50 || Ex: 4.6: Q 16 - 24 || Variation of Parameter Method
Maths Differential Equation part 16 (Homegeneous differential Equation) CBSE Mathematics XII 12
Комментарии
 1:11:01
1:11:01
 0:08:38
0:08:38
 0:28:21
0:28:21
 0:15:31
0:15:31
 0:04:43
0:04:43
 0:04:01
0:04:01
 0:03:38
0:03:38
 0:19:45
0:19:45
 0:04:02
0:04:02
 0:37:22
0:37:22
![[Numerical Modeling 16]](https://i.ytimg.com/vi/ZcckIrK-Oog/hqdefault.jpg) 0:17:45
0:17:45
 0:02:03
0:02:03
 0:02:37
0:02:37
 0:08:10
0:08:10
 0:32:37
0:32:37
 0:29:56
0:29:56
 0:03:18
0:03:18
 0:05:54
0:05:54
 0:15:01
0:15:01
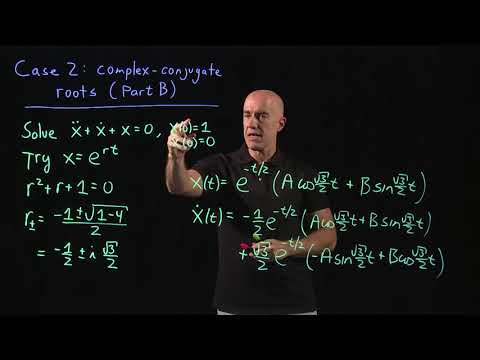 0:08:22
0:08:22
 0:08:23
0:08:23
 0:00:25
0:00:25
 0:36:12
0:36:12
 0:09:02
0:09:02