filmov
tv
🔵16 - Bernoulli Differential Equations (dy/dx + p(x)y = q(x)y^n)

Показать описание
In this video, we shall consider another method in solving differential Equations, we shall be looking at Bernoulli differential equations.
A Bernoulli Differential Equation is an equation of the form
dy/dx + p(x) = q(x)y^n, where both p and q are all functions of x.
Steps to solve Bernoulli DE
1. Rearrange the DE in the form: dy/dx + p(x)y = q(x)y^n
2. Find the integrating factor, u(x)
3. Solve for the general solution
00:00 - Ex 1
12:42 - Ex 2
Playlists on various Course
1. Applied Electricity
2. Linear Algebra / Math 151
3. Basic Mechanics
4. Calculus with Analysis / Calculus 1 / Math 152
5. Differential Equations / Math 251
6. Electric Circuit Theory / Circuit Design
Make sure to watch till the end.
Like, share, and subscribe.
Thank you.
A Bernoulli Differential Equation is an equation of the form
dy/dx + p(x) = q(x)y^n, where both p and q are all functions of x.
Steps to solve Bernoulli DE
1. Rearrange the DE in the form: dy/dx + p(x)y = q(x)y^n
2. Find the integrating factor, u(x)
3. Solve for the general solution
00:00 - Ex 1
12:42 - Ex 2
Playlists on various Course
1. Applied Electricity
2. Linear Algebra / Math 151
3. Basic Mechanics
4. Calculus with Analysis / Calculus 1 / Math 152
5. Differential Equations / Math 251
6. Electric Circuit Theory / Circuit Design
Make sure to watch till the end.
Like, share, and subscribe.
Thank you.
🔵16 - Bernoulli Differential Equations (dy/dx + p(x)y = q(x)y^n)
The Bernoulli Equation // Substitutions in Differential Equations
Bernoulli Differential Equations: Solution Methods and Exercises
How to Solve Bernoulli Differential Equations (Differential Equations 23)
Bernoulli’s Differential Equations
solving a hard Bernoulli differential equation
Bernoulli Differential Equations (MM-9.6-18)
Differential Equations - 17 - Bernoulli's Equation
BERNOULLI EQUATION || How to reduce it into the linear differential equation ?? || Mathematics ||
Solving Bernoulli Differential Equations Made Simple
Bernoulli Differential Equation x*dy/dx + y = 1/y^2
Bernoulli differential equations Example - 16(Bernolli diff. denklemleri Örnek -16)
Bernoulli's Method for Differential Equations
Differential equations: Bernoulli Equation
Bernoulli's Differential Equations - (Part 5) | Problems & Solutions
question 16 exercise 2.5 Dennis Gzill Michael Rcullen Bernoulli equation
Bernoulli's Equation
Bernoulli Differential Equations
16. Bernoulli’s Differential Equation – Part 2
Introduction to Bernoulli Differential Equations (Substitution)
Understanding Bernoulli's Differential Equation
First Order Bernoulli Differential Equations (Non-linear but can be made Linear)
Bernoulli's Equation
Bernoulli's Differential Equation [ Problem 1 ]
Комментарии
 0:28:21
0:28:21
 0:09:19
0:09:19
 0:11:16
0:11:16
 1:43:35
1:43:35
 0:17:05
0:17:05
 0:13:13
0:13:13
 0:01:38
0:01:38
 0:07:39
0:07:39
 0:07:26
0:07:26
 0:10:53
0:10:53
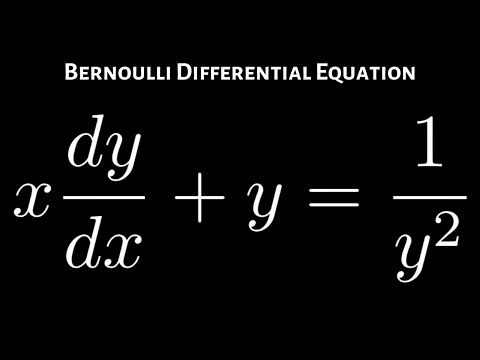 0:11:11
0:11:11
 0:06:26
0:06:26
 0:22:48
0:22:48
 0:08:51
0:08:51
 0:06:38
0:06:38
 0:03:31
0:03:31
 0:00:16
0:00:16
 0:06:03
0:06:03
 0:26:34
0:26:34
 0:05:30
0:05:30
 0:11:18
0:11:18
 0:41:54
0:41:54
 0:00:16
0:00:16
 0:15:46
0:15:46