filmov
tv
Dividing by zero?

Показать описание
Why can't you divide by zero? This lesson looks at why division by zero is not allowed - not only is the answer undefinable, but seriously, if you do do it, a whole bunch of people on youtube lose it.
Why can't you divide by zero? - TED-Ed
Dividing By Zero
Dividing by zero?
Dividing by Zero in Five Levels -- Elementary to Math Major
What happens when you divide by zero on a mechanical calculator?
Problems with Zero - Numberphile
Actually, you CAN divide by zero.
Dividing by zero on a soviet era calculator
Dividing by zero #maths #science
1 divided by 0 (a 3rd grade teacher & principal both got it wrong), Reddit r/NoStupidQuestions
I Learned How to Divide by Zero (Don't Tell Your Teacher)
Dividing by Zero!
Dividing by 0? #programming #computerscience
Divisibility - Dividing by 0
The real reason why you can’t divide a number by 0!! #math #maths #mathematics #shorts
Pete Parada of The Offspring performs 'Dividing By Zero'
Tried to divide by 0 😭😭😭
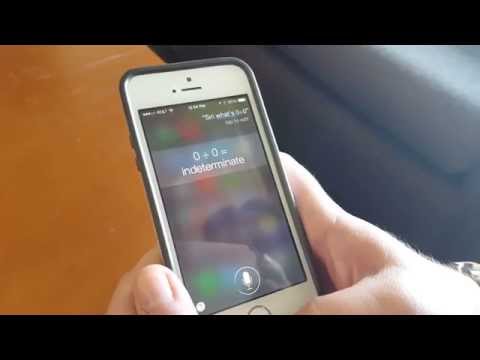
Sassy Siri: 'What's zero divided by zero?'
The REAL reason you can't divide by zero
How to Divide by 'Zero' | Infinite Series
Dividing Cake by Zero #math #zero #dividing #undefined
What Happens if you Divide by Zero on Different Calculators?
Why dividing by zero is undefined | Functions and their graphs | Algebra II | Khan Academy
When you divide by zero. CCC - Henry stickmin
Комментарии
 0:04:51
0:04:51
 0:02:23
0:02:23
 0:09:09
0:09:09
 0:06:49
0:06:49
 0:00:40
0:00:40
 0:13:00
0:13:00
 0:03:52
0:03:52
 0:00:24
0:00:24
 0:00:30
0:00:30
 0:04:52
0:04:52
 0:07:36
0:07:36
 0:08:34
0:08:34
 0:00:33
0:00:33
 0:01:40
0:01:40
 0:01:00
0:01:00
 0:02:48
0:02:48
 0:00:05
0:00:05
 0:00:21
0:00:21
 0:01:39
0:01:39
 0:13:23
0:13:23
 0:00:59
0:00:59
 0:08:20
0:08:20
 0:04:08
0:04:08
 0:00:24
0:00:24