filmov
tv
The REAL reason you can't divide by zero
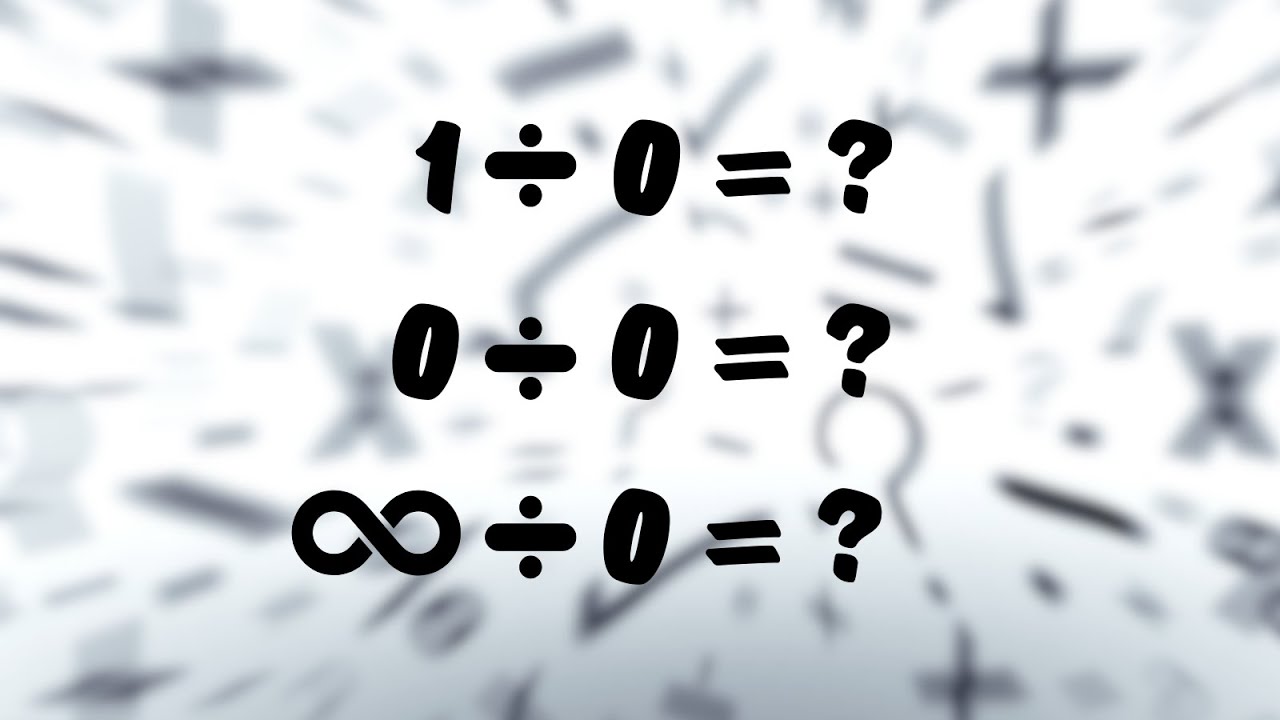
Показать описание
This video will walk you through the reasons why we avoid dividing by zero in maths.
Tags: #maths #learning #study #students #math #mathematics #puzzles #problemsolving #gcse
Tags: #maths #learning #study #students #math #mathematics #puzzles #problemsolving #gcse
The REAL Reason You Can't Afford a House
The Yerkes-Dodson Law; the REAL reason you can’t get stuff done!
The Real Reason You Can’t Slip Like Mike Tyson
The Real Reason You Can't Abstain from that One Addictive Sin in Your Life
The Real REASON Dhar Mann HASN'T POSTED...
THE REAL REASON YOU DON'T FIT IN (THIS IS SO POWERFUL)
The REAL reason you don’t get a charger anymore.
The Real Reason You Can't Get Inside and Land Punches in Boxing, MMA, Kickboxing and Muay Thai
The REAL Reason You Don't Have Abs yet- And Its Not Your Workout #gym #absworkout #abs
The Real Reason You Don't Get A Second Date
The Real Reason You Can't Get a Rolex at an AD in 2024! (The Waitlist's Dirty Little Secre...
The Psychology of Disorganization and Clutter / the real reasons you can't get organized or cle...
The REAL Reason You Can't Scale Facebook Ads
The Real Reason You Can't Change People
The Real Reason Putin Started War Against Ukraine – He Can't Live Without It
The REAL Reason Why People Don't Want To Work Anymore
TRUTH BOMB: The Real Reason You Can't Find Purpose (& 3 Things To Do Instead)
The REAL Reason You Can't Buy a House in Australia
the REAL reason why JVKE says you can't play 'GOLDEN HOUR' on piano...
Here’s The REAL Reason You Can’t Afford A House
Real Reason You Can't Fall Asleep
The Real Reason Why Many People Can’t Stand Jennifer Lopez |⭐ OSSA
The Real Reason You Can’t Find Peace in Your Life
THE REAL REASON YOU DON'T FIT IN (THIS IS SO POWERFUL) II
Комментарии
 0:10:04
0:10:04
 0:07:32
0:07:32
 0:09:49
0:09:49
 0:12:07
0:12:07
 0:11:43
0:11:43
 0:11:10
0:11:10
 0:13:03
0:13:03
 0:08:48
0:08:48
 0:00:51
0:00:51
 0:17:36
0:17:36
 0:03:51
0:03:51
 0:14:45
0:14:45
 0:10:20
0:10:20
 0:03:26
0:03:26
 0:06:06
0:06:06
 0:12:33
0:12:33
 0:09:34
0:09:34
 0:01:20
0:01:20
 0:04:36
0:04:36
 0:05:27
0:05:27
 0:18:06
0:18:06
 0:06:13
0:06:13
 1:01:34
1:01:34
 0:12:58
0:12:58