filmov
tv
Solving a Spectacular Factorial Equation | Algebra
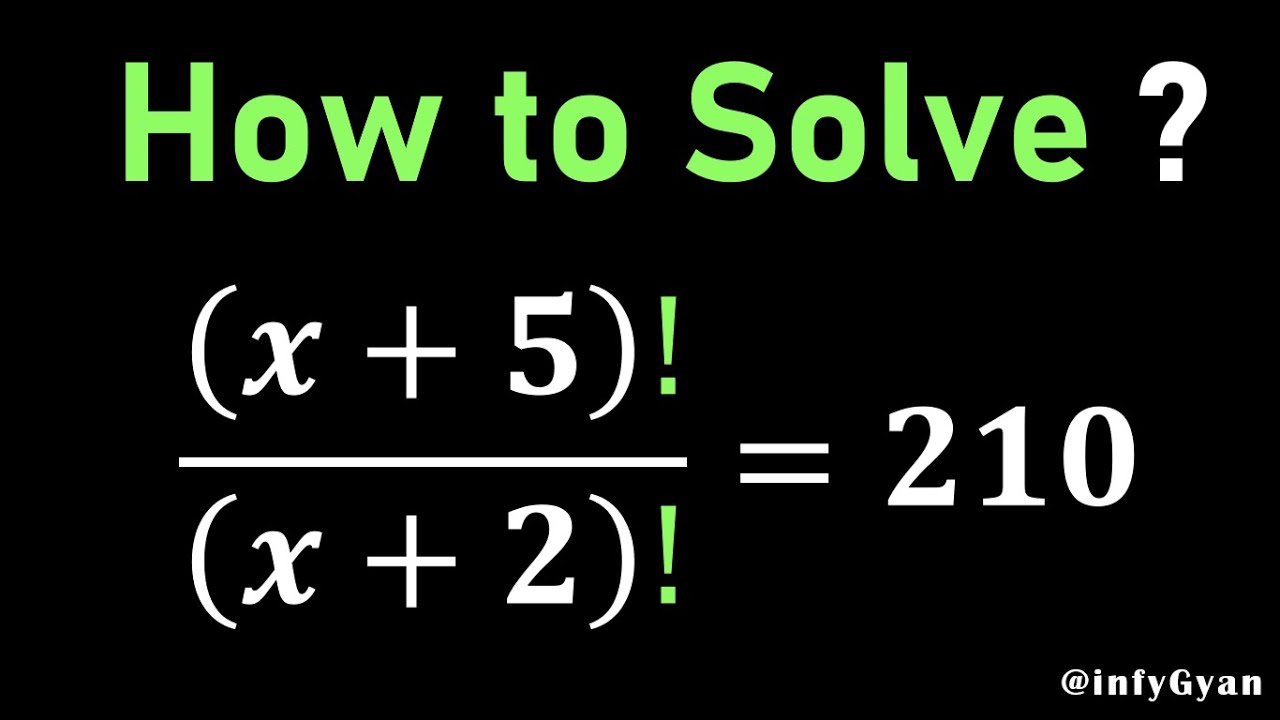
Показать описание
Solving a Spectacular Factorial Equation | Algebra
In this captivating video, we delve into the intriguing realm of factorial equations, unlocking their secrets and cracking the code to solve a truly spectacular factorial equation. Join us on a mathematical adventure as we unravel the complexities and reveal the step-by-step process to conquer this captivating challenge. With insightful explanations, factorials, cubic equation, remainder theorem and expert tips, you'll gain the knowledge and skills to confidently solve factorial equations and witness the remarkable power of factorials in action. Get ready to crack the factorial code and unravel the mysteries of this spectacular equation!
Topics Covered:
Algebra
Factorials
Solving Factorial equations
Cubic Equation
Remainder theorem
Quadratic equation
Quadratic formula
Algebra Challenge
8 Key moments of this video:
0:00 Introduction
0:36 Factorials
1:26 Cubic equation
3:45 Finding one factor
4:30 Remainder theorem
6:12 Quadratic equation
6:24 Quadratic formula (Discriminant)
7:38 Verification
#FactorialEquation
#EquationSolving
#FactorialCodeCracked
#MathAdventure
#MathTipsAndTricks
#MathEducation
#MathEnthusiast
#algebra
#math
#mathtutorial
#nonstandardequation
Do not forget to like, share and subscribe!!
Thanks for Watching!!
@infyGyan
In this captivating video, we delve into the intriguing realm of factorial equations, unlocking their secrets and cracking the code to solve a truly spectacular factorial equation. Join us on a mathematical adventure as we unravel the complexities and reveal the step-by-step process to conquer this captivating challenge. With insightful explanations, factorials, cubic equation, remainder theorem and expert tips, you'll gain the knowledge and skills to confidently solve factorial equations and witness the remarkable power of factorials in action. Get ready to crack the factorial code and unravel the mysteries of this spectacular equation!
Topics Covered:
Algebra
Factorials
Solving Factorial equations
Cubic Equation
Remainder theorem
Quadratic equation
Quadratic formula
Algebra Challenge
8 Key moments of this video:
0:00 Introduction
0:36 Factorials
1:26 Cubic equation
3:45 Finding one factor
4:30 Remainder theorem
6:12 Quadratic equation
6:24 Quadratic formula (Discriminant)
7:38 Verification
#FactorialEquation
#EquationSolving
#FactorialCodeCracked
#MathAdventure
#MathTipsAndTricks
#MathEducation
#MathEnthusiast
#algebra
#math
#mathtutorial
#nonstandardequation
Do not forget to like, share and subscribe!!
Thanks for Watching!!
@infyGyan
Комментарии
 0:08:36
0:08:36
 0:15:55
0:15:55
 0:04:14
0:04:14
 0:09:44
0:09:44
 0:02:36
0:02:36
 0:10:44
0:10:44
 0:11:26
0:11:26
 0:00:48
0:00:48
 0:06:01
0:06:01
 0:04:39
0:04:39
 0:03:39
0:03:39
 0:05:40
0:05:40
 0:04:12
0:04:12
 0:03:43
0:03:43
 0:06:26
0:06:26
 0:00:38
0:00:38
 0:18:10
0:18:10
 0:11:37
0:11:37
 0:09:19
0:09:19
 0:08:11
0:08:11
 0:00:11
0:00:11
 0:22:09
0:22:09
 0:09:49
0:09:49
 0:01:24
0:01:24