filmov
tv
An Amazing Factorial Equation Challenge | Can You Solve This?
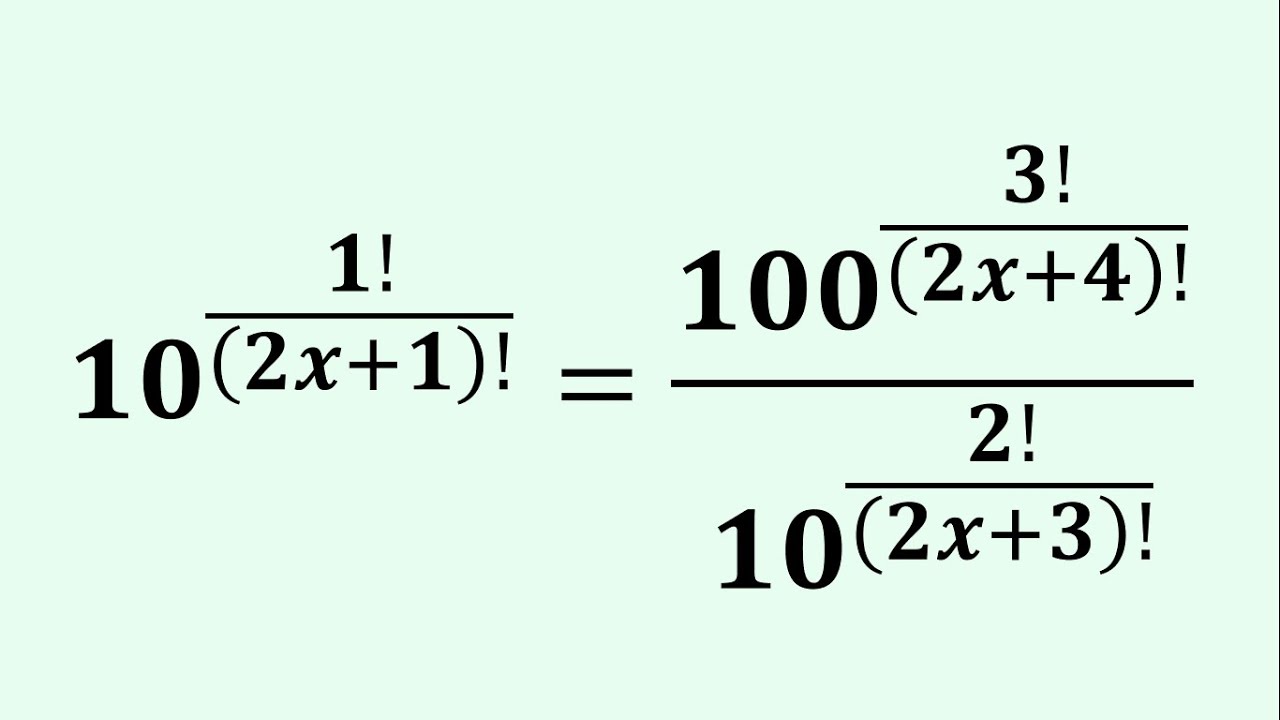
Показать описание
An Amazing Factorial Equation Challenge | Can You Solve This?
Join us in the algebraic video on an intriguing factorial exponential equation, perfect for Math Olympiad preparation! In this video, we explore the complexities and solutions of this challenging mathematical problem, offering insights and techniques essential for tackling Olympiad-level mathematics.
🌟 Subscribe for more Olympiad math challenges and solutions!
Topics covered:
Factorial equations
Exponential equation
Factorial
Factorial formula
How to solve exponential equations?
Algebra
Properties of exponents
Algebraic identities
Radicals
Factorial Exponential Equation
Math Olympiad preparation
Math Olympiad training
Exponent laws
Real solutions
Additional resources:
#factorial #exponentialequations #olympiadmath #mathematics #math #matholympiad #problemsolving #mathchallenge #radical #algebra
Don't forget to like this video if you found it helpful, subscribe to our channel for more Olympiad-focused content, and ring the bell to stay updated on our latest math-solving sessions.
Thanks for Watching !!
Join us in the algebraic video on an intriguing factorial exponential equation, perfect for Math Olympiad preparation! In this video, we explore the complexities and solutions of this challenging mathematical problem, offering insights and techniques essential for tackling Olympiad-level mathematics.
🌟 Subscribe for more Olympiad math challenges and solutions!
Topics covered:
Factorial equations
Exponential equation
Factorial
Factorial formula
How to solve exponential equations?
Algebra
Properties of exponents
Algebraic identities
Radicals
Factorial Exponential Equation
Math Olympiad preparation
Math Olympiad training
Exponent laws
Real solutions
Additional resources:
#factorial #exponentialequations #olympiadmath #mathematics #math #matholympiad #problemsolving #mathchallenge #radical #algebra
Don't forget to like this video if you found it helpful, subscribe to our channel for more Olympiad-focused content, and ring the bell to stay updated on our latest math-solving sessions.
Thanks for Watching !!
An Amazing Factorial Equation Challenge | Can You Solve This?
Solving the Unsolvable: Factorial Equation Challenge
Can You Beat This Factorial Equation Math Challenge?
Solving A Cool Factorial Equation: Math behind Solution
A Cool Factorial Equation Challenge-Calculators NOT Allowed
The Mind-Boggling Factorial Equation Challenge: Can You Solve It?
Can You Beat the Odds? Factorial Equation Challenge!
Factorial Challenge
Are You Up for the Factorial Equation Challenge?🤔
A nice factorial equation: The math behind solving equations.
Awesome!A Nice Factorial Equation|Math Olympiad Question!
Challenge Accepted: Can You Solve This Simple Factorial Equation?
Factorial Equation Challenge: Two Techniques for Success!
MIND-BLOWING Factorial Equation | An Easy Way to Solve it
Solving An Intriguing Factorial Equation Challenge!
Factorial Equation by Steve Hat | Math Challenge
Mastering Factorial Equations: Solving a Challenging Example
Math Olympiad Challenge | Can You Crack This Factorial Equation?
OMG 😳| Factorial and Exponent Challenge
A Cool Factorial Equation | CAT Challenge
Evaluate #shorts #factorial #maths #mathematics #challenge #olympiad #mathcompetition #short #viral
Mastering Factorial Equations: A Math Olympiad Challenge
Must try Maths Problem | Factorial Equation | Learn Factorial #maths
Factorial Equation Challenge: What is the Value of x in (3x - 4)! = 120? #factorial #maths
Комментарии
 0:15:55
0:15:55
 0:10:44
0:10:44
 0:10:26
0:10:26
 0:10:52
0:10:52
 0:11:15
0:11:15
 0:12:13
0:12:13
 0:10:00
0:10:00
 0:01:00
0:01:00
 0:08:31
0:08:31
 0:10:54
0:10:54
 0:06:02
0:06:02
 0:09:21
0:09:21
 0:14:46
0:14:46
 0:09:44
0:09:44
 0:09:25
0:09:25
 0:03:27
0:03:27
 0:09:00
0:09:00
 0:09:58
0:09:58
 0:00:28
0:00:28
 0:12:41
0:12:41
 0:01:00
0:01:00
 0:08:32
0:08:32
 0:00:41
0:00:41
 0:00:24
0:00:24