Solving the Unsolvable: Factorial Equation Challenge

Показать описание

Solving the Unsolvable: Factorial Equation Challenge

Join us on an exhilarating mathematical journey as we take on the unsolvable – the Factorial Equation Challenge! 🧮💡 We'll explore complex mathematical equations involving factorials, apply clever strategies, and work through some mind-bending examples. Whether you're a math enthusiast or looking to level up your algebra skills, this video is sure to spark your curiosity and test your problem-solving abilities. Can you solve the unsolvable? Let's find out together! 🔍✨

You will learn:
1. Factorial Equations
2. Olympiad Exam
3. Mathematics
4. Problem Solving
5. Value of X
6. Exam Preparation
7. Math Tutorial
8. Step-by-Step Guide
9. Math Olympiad
10. Algebraic identities
11. Math Olympiad Preparation
12. Factorial notation
13. Recursive formula

8 Key moments of this video:
0:00 Introduction
0:32 Factorials
0:58 Recursive formula
2:23 Algebraic identities
4:50 Substitution
6:30 Algebraic expansion
8:16 Logical conclusions
10:08 Verification

#Mathematics #FactorialEquation #MathChallenge #Algebra #ProblemSolving #MathEnthusiasts #Factorials #EquationSolving #MathJourney #UnsolvableChallenge #MathSkills #AlgebraicPuzzles #Curiosity #MathematicalExploration #MindBendingMath #FactorialMath #LearnMath #MathPuzzles #MathFun #MathProblems #AlgebraSkills
#algebra #math #factorials #mathematics #infyGyan

Channel link for more perks:

Do not forget to like, share and subscribe !!

Thanks for watching!

Рекомендации по теме

Комментарии

(x + 2)! + x^3 = x^5

Thus, x => -2 and is an integer

If x = -2, then 0! + (-8) != (-32)
If x = -1, then 1! + (-1) != (-1)
If x = 0, then 2! + 0 != 0
If x = 1, then 3! + 1 != 1
If x = 2, then 4! + 8 = 32 so x = 2 is a solution.

Now suppose x => 3.

(x + 2)! = x^5 - x^3
(x + 2)! = x^3 (x^2 - 1)
(x + 2)! = x^3 (x - 1)(x + 1)
(x + 2)(x + 1)(x)(x - 1)(x - 2)(x - 3)! = x^3 (x - 1)(x + 1)
(x + 2)(x - 2)(x - 3)! = x^2
(x^2 - 4)(x - 3)! = x^2
(x - 3)! = x^2 / (x^2 - 4)
(x - 3)! = 1 + 4 / (x^2 - 4)
(x - 3)! - 1 = 4 / (x^2 - 4)

Since x => 3, then
x^2 => 9
x^2 - 4 => 5 > 4
x^2 - 4 > 4
4 / (x^2 - 4) < 1

The LHS is an integer and the RHS is between 0 and 1, a contradiction.

Thus, x = 2 is the only solution

Packerfan

Real men would solve this with the gamma function

ShadowGamingof

thank you so much sir, I love you man

MAARSHN

how does this video only have 21 likes this is beautiful

mahadkhan

Solving the Unsolvable: Factorial Equation Challenge

Solving the Unsolvable: Factorial Equation Challenge

5 simple unsolvable equations

The Simplest Math Problem No One Can Solve - Collatz Conjecture

Fun Factorial Problem

How to Take the Factorial of Any Number

A Factorial Equation | Algebra #maths

Mastering Factorial Equations: Solving a Challenging Example

Solve the Unsolved Are You Smart Enough to Simplify this Factorial Fraction #igcse #maths

Zero Factorial Explained: The Math Behind Why 0! is 1

Why There's 'No' Quintic Formula (proof without Galois theory)

Extending the FACTORIAL! Gamma function derived in 60 seconds!

Can You Solve this Equation Consist of Factorial as Variable | Tricky Math Problem

Big Factorials - Numberphile

The problem in Good Will Hunting - Numberphile

solving equations but they get increasingly more impossible?

Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths

Solving the hardest question of a British Mathematical Olympiad

Why is this 15-Puzzle Impossible? - Numberphile

How fast are you able to solve this factorial question? #computerscience #coding #stem #shorts

Luxembourg - Math Olympiad Question | You should know this trick

Factorial (!) ? | Fun Math | Don't Memorise

The Riddle That Seems Impossible Even If You Know The Answer

I Computed An Integral That Breaks Math

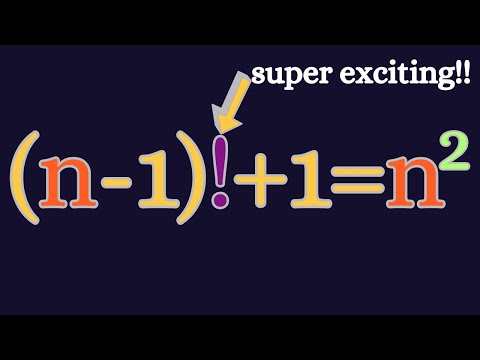a nice factorial equation.