both SEPARABLE & LINEAR differential equation

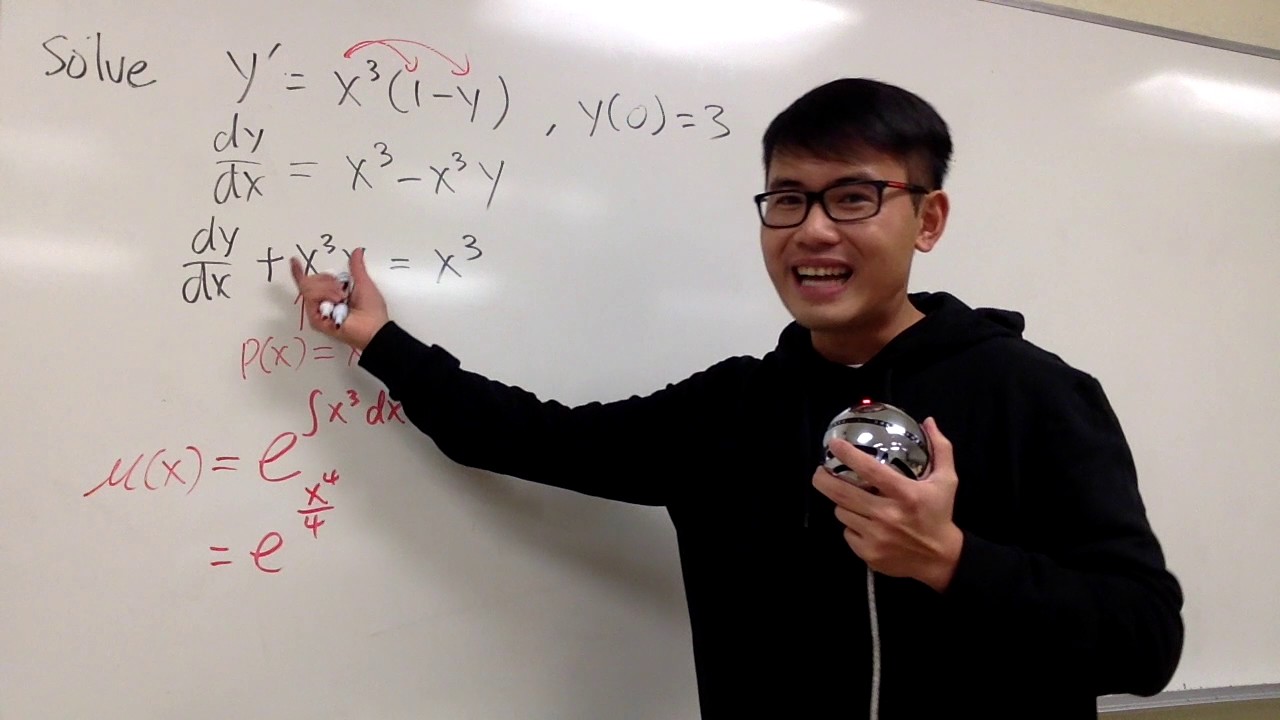
Показать описание

Part1 of Differential Equation Course: How to solve first order differential equations? The topics/technique include:

separable differential equations,
first order linear differential equations,
integrating factor,
exact differential equations,
special integrating factor,
solve differential equations by substitution,
homogeneous differential equations,
bernoulli differential equation,

(this playlist provides the ideas behind each kind of diff eq, the strategies to solve each kind of diff eq, and plenty of examples/homework examples)

YOU CAN'T SOLVE DIFFERENTIAL EQUATION WITHOUT KNOWING YOUR INTEGRALS!

blackpenredpen
separable differential equations,
first order linear differential equations,
integrating factor,
exact differential equations,
special integrating factor,
solve differential equations by substitution,
homogeneous differential equations,
bernoulli differential equation,

(this playlist provides the ideas behind each kind of diff eq, the strategies to solve each kind of diff eq, and plenty of examples/homework examples)

YOU CAN'T SOLVE DIFFERENTIAL EQUATION WITHOUT KNOWING YOUR INTEGRALS!

blackpenredpen

Рекомендации по теме

Комментарии

The background music cures my depression

shobhitmishra

Thank you for an awesome video on both Separable and Linear Differential Equations.

georgesadler

Elementary School: *_"S h O W Y o U R W O r K!"_*
Middle School: *_"s H o w y O u r w o R k!!"_*
High School: *_"S H O W Y O U R W O R K!!!"_*

bprp: *"the best way you can do these kinds of things is look at this and do the integral - do the U-Substitution - in your head"* 🙂🙃

isaackay

Thanks for the vid! I'll be starting my differential equations class this semester.

scottryder

do you have videos for eliminating arbitrary constant?

shaunhugo

Why bother using a integrable factor? Can't you just use substitution?

y' = x^3*(1-y)

u = 1 - y
y = 1 - u
dy/dx = -du/dx
y' = -u'

- u' = x^3*u
u' = -x^3*u
u'/ u = -x^3
ln u = -x^4/4 + c_1
u = e^(-x^4/4 + c_1)
u = e^(-x^4/4)*e^c_1

y = 1 - u
y = 1 - e^(-x^4/4)*e^c_1

e^c_1 = c
y = 1 - c*e^(-x^4/4)
3 = 1 - c*1
2 = -c
c = -2
y = 1 + 2e^(-x^4/4)

The only weirdness lies in trying to solve for c_1. e^c_1 = -2. I suppose c_1 can be complex, but I don't think integration prohibits imaginary constants.

tsujimasen

both SEPARABLE & LINEAR differential equation

both SEPARABLE & LINEAR differential equation

Separable First Order Differential Equations - Basic Introduction

both SEPARABLE & LINEAR differential equation

4 Types of ODE's: How to Identify and Solve Them

First Order Linear Differential Equations

Separable Differential Equation (introduction & example)

Separation of Variables // Differential Equations

Separable differential equations introduction | First order differential equations | Khan Academy

L44 KCET 2025 Maths Course | Differential Equation- 3 | Linear Differential Eq & PYQs

Identify the type of differential equations such as separable, linear, Bernoulli’s etc.

Basic First Order Separable Linear Differential Equation

Separable Differential Equations (Differential Equations 12)

Second Order Linear Differential Equations

Worked example: separable differential equation (with taking exp of both sides) | Khan Academy

❖ Solving Separable First Order Differential Equations ❖

Separable and linear differential equation examples

Worked example: identifying separable equations | AP Calculus AB | Khan Academy

Isolating variables for two different separable differential equations.

Mixing Salt and Water - First Order Differential Equations

A beautiful separable differential equation

How to solve separable differential equations

Separable differential equation with initial condition

How to Solve First Order Linear Differential Equations

Separable Differential Equations? How to solve separable differential equations? Lec # 04