filmov
tv
what's the integral of 1/x from -1 to 1

Показать описание
The Integral of 1/x EXPLAINED. It's NOT what you think...
Integral of 1/x
what's the integral of 1/x from -1 to 1
Why is the integral of 1/x equal to ln(x)+C? Reddit r/calculus
Integration : 1/x and 1/(ax+b) types : ExamSolutions
Indefinite integral of 1/x | AP Calculus AB | Khan Academy
Improper integral of 1/x from -1 to 1 (THE DEBATE?)
Using my Integral Formula to Integrate 1/(x^n+1)
Final Exam Review : Calculus 2 Part 12
Integral of 1/(1+x^2)
How REAL Men Integrate Functions
Calculus SPEEDRUN (U-Sub)!!
how Richard Feynman would integrate 1/(1+x^2)^2
integral of 1/(x^3+x), partial fraction or MAYBE NOT
This is all Integration is (quickfire AI lesson)
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
Is this integral 0?
Quick solution to integral 1/(1+x^4)
Indefinite Integral of 1/x^2
Integral of 1/x
Integral of 1/(1+e^x)
Integration Basic Formulas
The Most Useful Calculus 1 Tip!
Differentiation and integration important formulas||integration formula
Комментарии
 0:03:12
0:03:12
 0:00:50
0:00:50
 0:04:01
0:04:01
 0:05:28
0:05:28
 0:15:12
0:15:12
 0:07:35
0:07:35
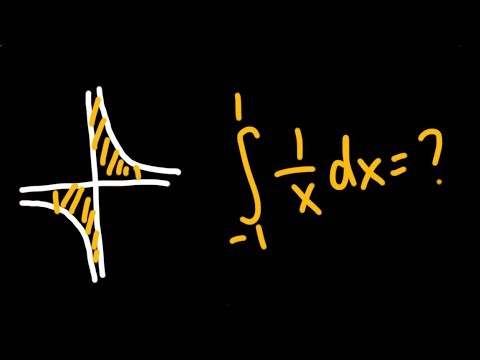 0:11:59
0:11:59
 0:00:12
0:00:12
 11:53:05
11:53:05
 0:02:29
0:02:29
 0:00:35
0:00:35
 0:01:00
0:01:00
 0:08:53
0:08:53
 0:11:30
0:11:30
 0:00:59
0:00:59
 0:00:09
0:00:09
 0:00:55
0:00:55
 0:01:55
0:01:55
 0:10:09
0:10:09
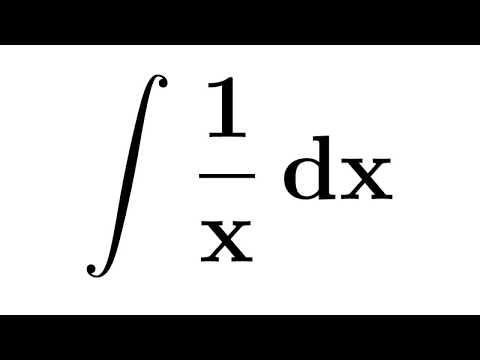 0:03:41
0:03:41
 0:00:58
0:00:58
 0:00:05
0:00:05
 0:00:10
0:00:10
 0:00:16
0:00:16