filmov
tv
Integral of 1/x

Показать описание
A quick afternoon integral, ep4.
------------------------------------------------------------------------------------
bprp #shorts
------------------------------------------------------------------------------------
bprp #shorts
The Integral of 1/x EXPLAINED. It's NOT what you think...
Why is the integral of 1/x equal to ln(x)+C? Reddit r/calculus
Integration : 1/x and 1/(ax+b) types : ExamSolutions
Indefinite integral of 1/x | AP Calculus AB | Khan Academy
Improper integral of 1/x from -1 to 1 (THE DEBATE?)
what's the integral of 1/x from -1 to 1
Integral of 1/(1+x^2)
Integral of 1/x
Integration of 1/(√(x+1) - √(x)) | Integral Calculus
How to integrate 1/x^2
Integral of 1/(x^3+1) from 100 integrals
Indefinite Integral of 1/x^2
Integral of 1/x from 0 to 1
Definite Integral of 1/x from 1 to 2
Integral of 1/x from 1 to Infinity
Integration of Rational Functions into Logarithms By Substitution & Long Division
Definite Integral of 1/x from -2 to -1
I Computed An Integral That Breaks Math
Integral of 1/e^x
Integral of 1/e^x
Integral of 1/(1+e^x)
integral of 1/(x^2+1) but you didn't learn it this way in calculus 2
How REAL Men Integrate Functions
Ln(x) und 1/x und ihre Stammfunktionen, Logarithmusfunktion | Mathe by Daniel Jung
Комментарии
 0:03:12
0:03:12
 0:05:28
0:05:28
 0:15:12
0:15:12
 0:07:35
0:07:35
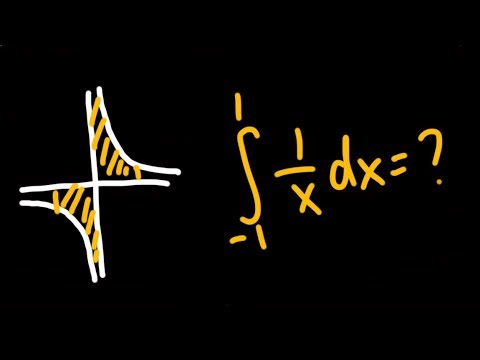 0:11:59
0:11:59
 0:04:01
0:04:01
 0:02:29
0:02:29
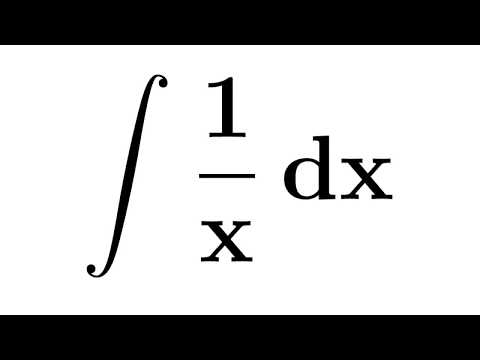 0:03:41
0:03:41
 0:00:00
0:00:00
 0:01:07
0:01:07
 0:13:19
0:13:19
 0:10:09
0:10:09
 0:03:39
0:03:39
 0:01:16
0:01:16
 0:01:34
0:01:34
 0:19:20
0:19:20
 0:01:37
0:01:37
 0:04:20
0:04:20
 0:00:41
0:00:41
 0:01:51
0:01:51
 0:03:08
0:03:08
 0:09:21
0:09:21
 0:00:35
0:00:35
 0:03:22
0:03:22