filmov
tv
Improper integral of 1/x from -1 to 1 (THE DEBATE?)
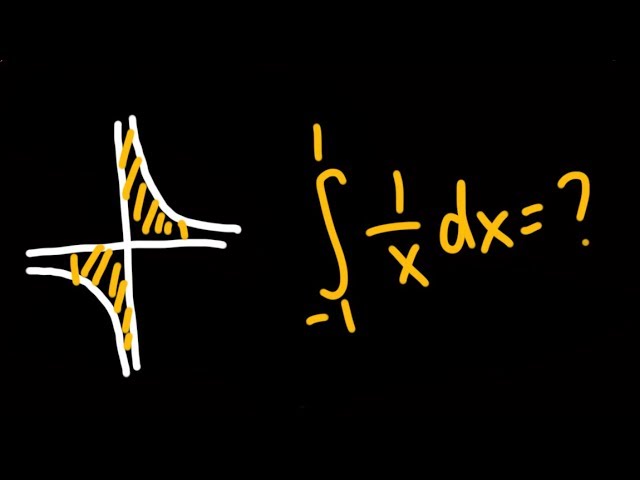
Показать описание
The debate of the improper integral of 1/x from -1 to 1. Is this zero or divergent?
Let me know what you think!
blackpenredpen
Let me know what you think!
blackpenredpen
Improper integral of 1/x from -1 to 1 (THE DEBATE?)
Improper Integrals - Convergence and Divergence - Calculus 2
Sect 7 8#31, improper integral of 1/x^4 from -2 to 3
Improper Integral of 1/x^2 from 2 to infinity
improper integral 1/x^3 from 1 to infinity | how to solve improper integrals | silent integrals
improper integral of 1/x from 1 to infinity | solving improper integrals | silent integrals
The p-integral Proof (type 1 improper integral)
Integral of 1/x from 1 to Infinity
Integral of the Day 10.18.24 | Another IMPROPER INTEGRAL for you to solve! | Math with Professor V
Improper integral of 1/x from 1 to infinity.
Integral of 1/x
6.6 Improper Integrals - Intro and HW#1, 2: integral of 1/x vs 1/x^2 (P-integrals Theorem)
improper integral from 0 to 2 of 1/(x-1)
Improper Integral of 1/(1+x^2) from Negative Infinity to Positive Infinity (-inf to +inf)
Integral of 1/x from 0 to 1
Improper Integral of 1/(x^2+1) with a = -inf and b = inf. (Calculus 2, Improper Integral)
Evaluating An Improper Integral
The Improper Integral of 1/x^(2/3) from -1 to 1
what's the integral of 1/x from -1 to 1
Improper Integral of 1/x^p
The Improper Integral of 1/sqrt(x) from 0 to 1
Comparison test for improper integrals ex 3, integral of 1/ln(x) from e to inf, calculus 2 tutorial
Type 1 improper integrals! calculus 2
Improper Integrals - Convergent or Divergent (Made Easy)
Комментарии
 0:11:59
0:11:59
 0:13:56
0:13:56
 0:02:58
0:02:58
 0:03:21
0:03:21
 0:01:26
0:01:26
 0:01:21
0:01:21
 0:08:31
0:08:31
 0:01:34
0:01:34
 0:06:07
0:06:07
 0:02:40
0:02:40
 0:00:50
0:00:50
 0:27:55
0:27:55
 0:07:13
0:07:13
 0:13:14
0:13:14
 0:03:39
0:03:39
 0:07:04
0:07:04
 0:00:54
0:00:54
 0:04:34
0:04:34
 0:04:01
0:04:01
 0:06:33
0:06:33
 0:02:37
0:02:37
 0:11:07
0:11:07
 0:27:48
0:27:48
 0:23:17
0:23:17