filmov
tv
Number Theorem | Gauss' Theorem
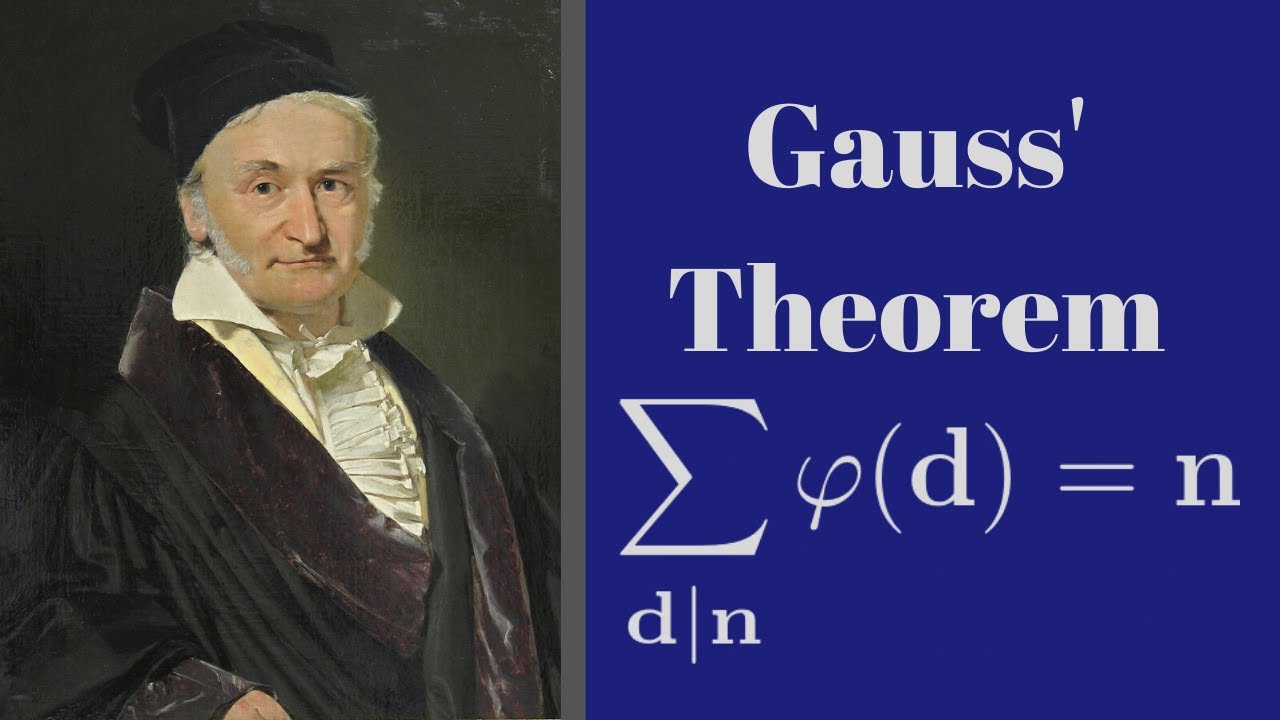
Показать описание
We prove Gauss's Theorem. That is, we prove that the sum of values of the Euler phi function over divisors of n is equal to n.
Number Theorem | Gauss' Theorem
Gauss Divergence Theorem. Get the DEEPEST Intuition.
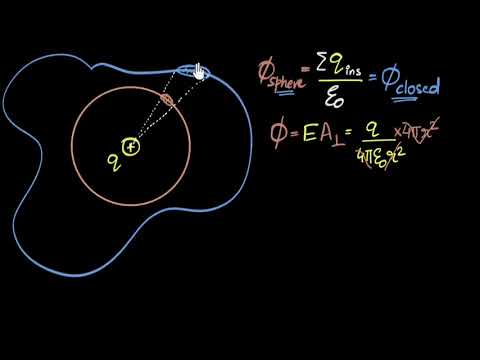
Gauss's Divergence Theorem
The Divergence Theorem
Number Theory | Gauss' Lemma
Number Theory 37: Gauss theorem
The High Schooler Who Solved a Prime Number Theorem
Gauss theorem || Gauss law physics || Abhishek sir
Electrostatic Gauss law and It's Applications | Class 12th Physics | Physics by Pragya Ma'...
Number Theory 38: Gauss theorem example with n=20
The Divergence Theorem, a visual explanation
Theorem of Gauss | 8th Class Mathematics | Digital Teacher
Gauss Lucas Theorem: The Roots Are Where?
The Divergence Theorem // Geometric Intuition & Statement // Vector Calculus
GAUSS THEOREM (NUMBER THEORY)
Proof & Explanation: Gauss's Lemma in Number Theory
Gauss Lemma {Number Theory} | problem 2
Pi hiding in prime regularities
Gauss Lemma [Number Theory] | how to calculate n for Gauss Lemma | 1
The Riemann Hypothesis, Explained
Add the Numbers from 1 to 100 like a 5-Year-Old! The Story of Gauss | Minute Math
Why did they prove this amazing theorem in 200 different ways? Quadratic Reciprocity MASTERCLASS
Gauss law logical proof (any closed surface) | Electric charges & fields | Physics | Khan Academ...
Gauss's law || full visual explanation || 12th physics
Комментарии
 0:09:03
0:09:03
 0:07:53
0:07:53
 0:26:53
0:26:53
 0:06:31
0:06:31
 0:12:19
0:12:19
 0:06:54
0:06:54
 0:05:15
0:05:15
 0:05:18
0:05:18
 1:22:20
1:22:20
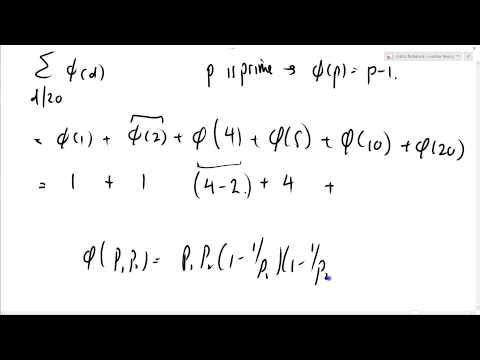 0:04:01
0:04:01
 0:12:51
0:12:51
 0:00:48
0:00:48
 0:11:09
0:11:09
 0:07:35
0:07:35
 0:10:54
0:10:54
 0:15:11
0:15:11
 0:03:45
0:03:45
 0:30:42
0:30:42
 0:03:28
0:03:28
 0:16:24
0:16:24
 0:03:10
0:03:10
 0:56:37
0:56:37
 0:12:16
0:12:16
 0:04:24
0:04:24