filmov
tv
Vieta's formulas with examples
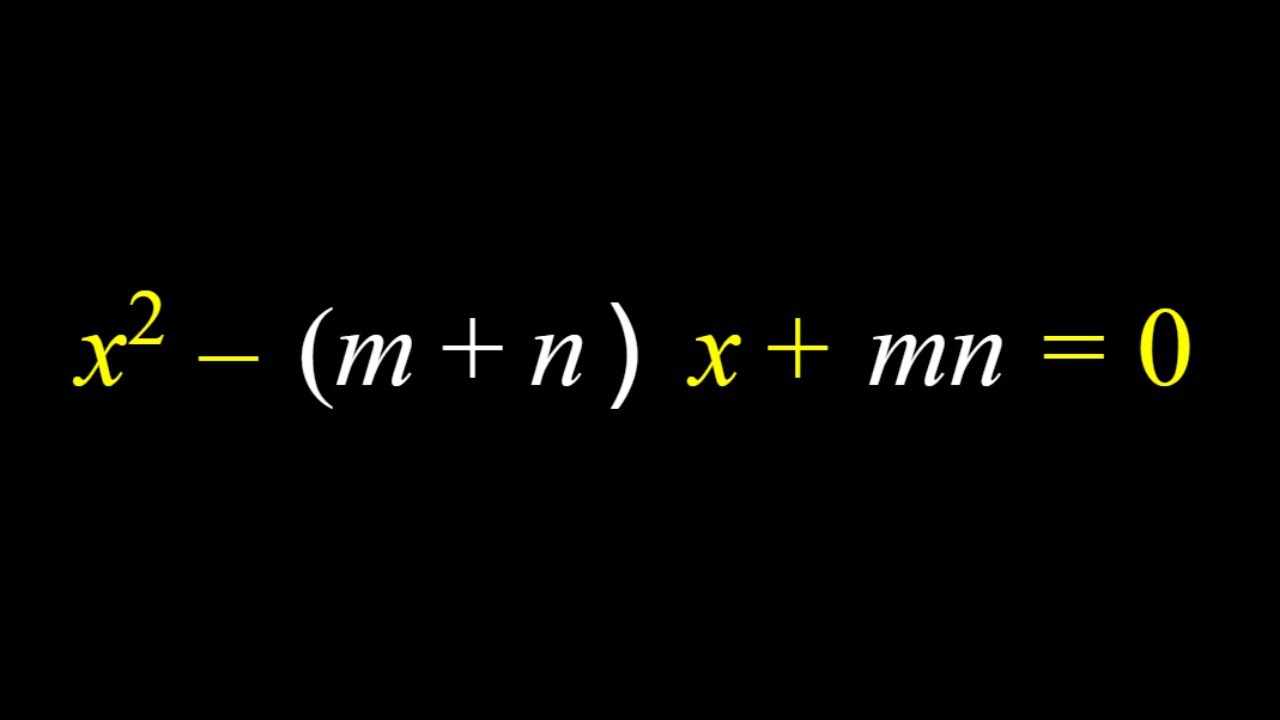
Показать описание
This video is about Vieta's formulas. I included a good variety of problems.
Send me a tweet at @SyberMath if you want to share a picture of your solution/ideas and comment here with the link to the tweet.
#NumberTheoryProblems #VietasFormulas
Send me a tweet at @SyberMath if you want to share a picture of your solution/ideas and comment here with the link to the tweet.
#NumberTheoryProblems #VietasFormulas
Vieta's Formula
Vieta's Formula for Quadratics: Proof & Examples
Vieta's formulas with examples
Vieta's formulas with Examples
Art of Problem Solving: Vieta for Quadratics Part 1
#vieta #formula #cubic #mathshorts
Cubic Factoring using Vietas Formula
Vieta's Formula: a simple example
Vieta's Formula
Vieta's Formulas - Mastering AMC 10/12
A Quadratic Equation and Its Roots | Vieta's Formulas
General Vieta's Formulas for Polynomials
How to solve these vieta formula questions!!! #maths #math
Cubic with Vieta's formula
Vieta's Formulas for quadratic equation and guessing roots - high school algebra
Using Vieta's Formulas
Vieta's Formula (Quadratic Equations Made Easy!) | Algebra
Sum of roots: Vieta Formula #maths #matematicas #algebra
Vieta's Formulas for Cubic Polynomials - Thursday Tidbit
Can you solve using Vieta's formula?
Application of Vieta's Formula
Vieta's Formulas
Vieta's Theorem for quadratic equation & Deriving Quadratic Equation 🔥 @infinityjunction
Vieta's Formula - Introduction
Комментарии
 0:14:34
0:14:34
 0:05:38
0:05:38
 0:27:08
0:27:08
 0:27:08
0:27:08
 0:09:16
0:09:16
 0:00:03
0:00:03
 0:20:16
0:20:16
 0:05:33
0:05:33
 0:11:03
0:11:03
 0:15:40
0:15:40
 0:00:35
0:00:35
 0:13:49
0:13:49
 0:00:35
0:00:35
 0:05:02
0:05:02
 0:06:39
0:06:39
 0:00:52
0:00:52
 0:05:47
0:05:47
 0:00:12
0:00:12
 0:09:56
0:09:56
 0:05:19
0:05:19
 0:02:19
0:02:19
 0:14:07
0:14:07
 0:04:08
0:04:08
 0:15:23
0:15:23