filmov
tv
Cubic with Vieta's formula
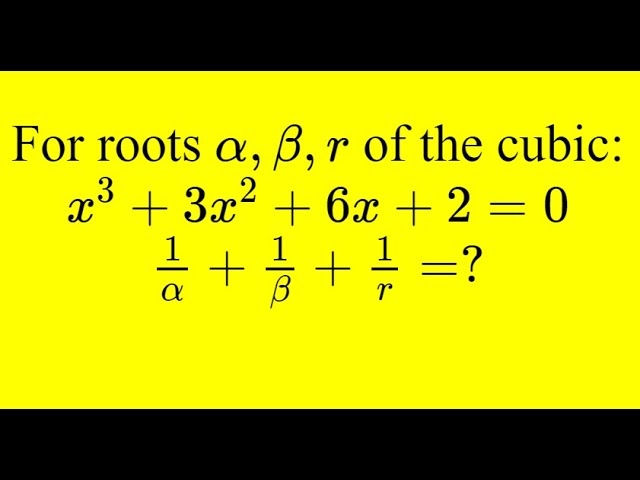
Показать описание
I solve the problem using Vieta's Formula
Related quizzes:
Related quizzes:
Cubic Factoring using Vietas Formula
Vieta's Formulas for Cubic Polynomials - Thursday Tidbit
Introduction to Vieta's Formula: Cubic Equations (Sum and Product of Roots)
Cubic with Vieta's formula
Vieta's Formulas for Cubic Equations
A nice problem on a cubic equation (ft. Vieta's Formula) || High School Math
#vieta #formula #cubic #mathshorts
Vieta's Formula Application Find Sum of Reciprocal of Roots for Cubic Equation
Find Cubic Polynomials Equation with Given Complex Root Vietas Formula Application
Using Vieta's formulas In a Cubic Equation
Using Vieta's Formulas in A Cubic Equation
Vieta's formulas for Cubic Polynomials
How to Find a Solution to a Cubic Equation
Vieta's formulas in a cubic equation
Vieta's formula for cubic equations
A Fun Way to Solve Cubics: Vieta's Substitution
Viète's Results: Cubic & General Polynomials
Application of Vieta's Formula
Using Vieta's Formulas on a Cubic Equation
Vieta's Formula
Vieta's Formulas
Vieta's formula
Using Vieta's Formula
Watch this to learn Cubic polynomials and Vieta's Relations
Комментарии
 0:20:16
0:20:16
 0:09:56
0:09:56
 0:07:55
0:07:55
 0:05:02
0:05:02
 0:07:07
0:07:07
 0:05:00
0:05:00
 0:00:03
0:00:03
 0:07:47
0:07:47
 0:08:46
0:08:46
 0:14:02
0:14:02
 0:00:33
0:00:33
 0:06:32
0:06:32
 0:01:56
0:01:56
 0:14:02
0:14:02
 0:04:30
0:04:30
 0:15:26
0:15:26
 0:03:07
0:03:07
 0:02:19
0:02:19
 0:09:09
0:09:09
 0:14:34
0:14:34
 0:14:07
0:14:07
 0:06:57
0:06:57
 0:05:47
0:05:47
 0:06:26
0:06:26