filmov
tv
Exponential Equation With Double Exponents | How To Solve Exponential Equations | Math Olympiad
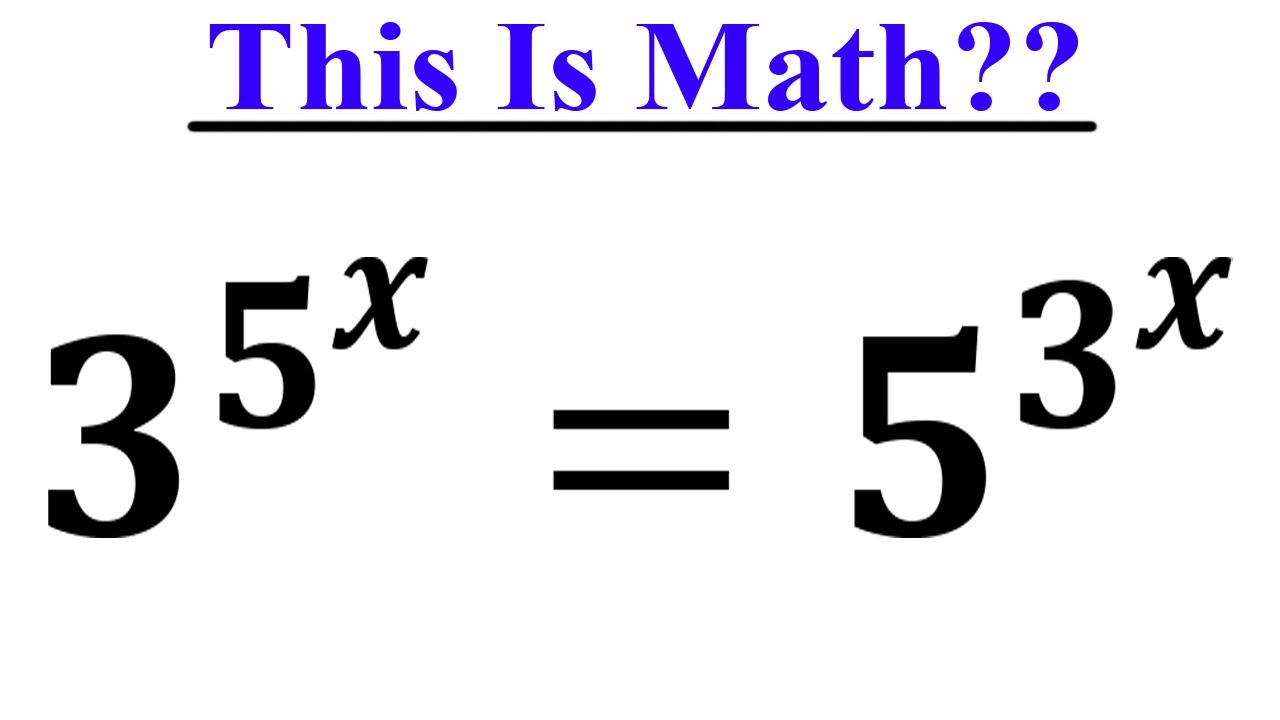
Показать описание
In this math algebra video, we shall solve an exponential equation with double exponents.
Exponential Equation With Double Exponents | How To Solve Exponential Equations | Math Olympiad
How to solve Exponential Equation with different variables as exponents
how to solve an exponential equation with two different bases
Two Ways to Solve this Exponential Equation @KasyannoEZMath
Exponential Equations - Algebra and Precalculus
How To Solve an Exponential Equation with Double Exponents | SAT Exam | Math | Algebra
Solving Simultaneous With Exponential directly.
How to solve an exponential equation with two different bases
Exponential equation | The two methods used
Beautiful Solution to a Difficult Exponential Equation with Two Variables x and y | Math Olympiad
How to simplify a power to a power. What does 2^2^3 really mean?
How do I find x? Exponential equation with two different bases. Reddit precalculus r/Homworkhelp
Solving Exponential Equation in Two Ways @KasyannoEZMath
Solving Exponential Equation
How to solve an exponential equation with two different bases
Learn How to Solve Exponential Equations Using Two Different Methods | Step-by-Step Tutorial
Ex 5: Solve Exponential Equations with Two Exponential Parts Using Logarithms
Solve an Exponential Equation | jensenmath.ca #maths #math #exponents
A FUN and CREATIVE exponent equation
Solving Exponential Equation
solving a double exponential equation
Solving Exponential Equations
Simplifying Exponents With Fractions, Variables, Negative Exponents, Multiplication & Division, ...
Exponent Formulas #maths #exponents
Комментарии
 0:03:20
0:03:20
 0:05:54
0:05:54
 0:03:21
0:03:21
 0:12:57
0:12:57
 0:05:58
0:05:58
 0:03:38
0:03:38
 0:13:50
0:13:50
 0:05:11
0:05:11
 0:03:54
0:03:54
 0:06:09
0:06:09
 0:04:01
0:04:01
 0:07:47
0:07:47
 0:14:19
0:14:19
 0:00:56
0:00:56
 0:05:50
0:05:50
 0:12:15
0:12:15
 0:05:41
0:05:41
 0:00:42
0:00:42
 0:00:54
0:00:54
 0:00:54
0:00:54
 0:05:02
0:05:02
 0:16:36
0:16:36
 0:11:48
0:11:48
 0:00:08
0:00:08