filmov
tv
Find the maximum value of n

Показать описание
This problem was a mathematics competition. The strategy is to complete thew square and use the properties of integers to find the maximum of of n
How to Find the Maximum or Minimum Value of Quadratic Functions
Determine if a quadratic has a max or min value then find it (mistake)
How to Find the Maximum or Minimum Value of a Quadratic Function Easily
Finding Local Maximum and Minimum Values of a Function - Relative Extrema
Find the maximum value of n
Finding Absolute Maximum and Minimum Values - Absolute Extrema
Find maximum element in an array (Largest element)
Excel Find the Min and Max Value in a Column using Conditional Formatting
How to find maximum number in excel #excel #exceltips #computer #hacks #shorts #new
EAF #23 - Find the Max value in a dataset using criteria - MAX IF Array formula
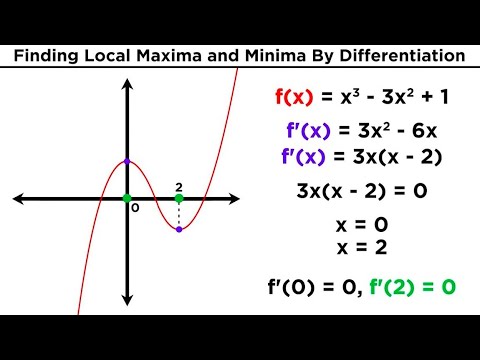
Finding Local Maxima and Minima by Differentiation
Learning how to find the maximum value of an objective function
To find Maximum and Minimum of a functions || Applications of derivatives
The maximum value of (1/x) ^x
Power BI Tutorial for finding Maximum Value and Creating New Measure using DAX MAX Function
How to find maximum value in a column Using MAX, MATCH and ADDRESS Function in Excel
Absolute Maximum and Minimum Values - Finding absolute MAX & MIN of Functions - Calculus
TI84 TI83 Finding Relative Maximum & Minimum
Identifying The Relative Maximum and Minimum Values of a Function
How to find and return maximum or minimum absolute value and keep sign in Excel?
Absolute Maximum and Minimum Values of Multivariable Functions - Calculus 3
How to Find the Maximum Value of Multiple Fields in the Same Record in Microsoft Access
Maximum and Minimum Values of a Quadratic Function
Finding the Minimum or Maximum of Quadratic Functions
Комментарии
 0:04:55
0:04:55
 0:04:54
0:04:54
 0:02:59
0:02:59
 0:14:18
0:14:18
 0:16:16
0:16:16
 0:17:17
0:17:17
 0:05:42
0:05:42
 0:04:32
0:04:32
 0:00:15
0:00:15
 0:09:49
0:09:49
 0:06:17
0:06:17
 0:09:00
0:09:00
 0:08:59
0:08:59
 0:03:11
0:03:11
 0:04:32
0:04:32
 0:03:04
0:03:04
 0:09:15
0:09:15
 0:02:24
0:02:24
 0:03:47
0:03:47
 0:05:37
0:05:37
 0:11:24
0:11:24
 0:18:33
0:18:33
 0:06:20
0:06:20
 0:07:22
0:07:22