filmov
tv
Connecting these Two Integrals with Integration by Parts
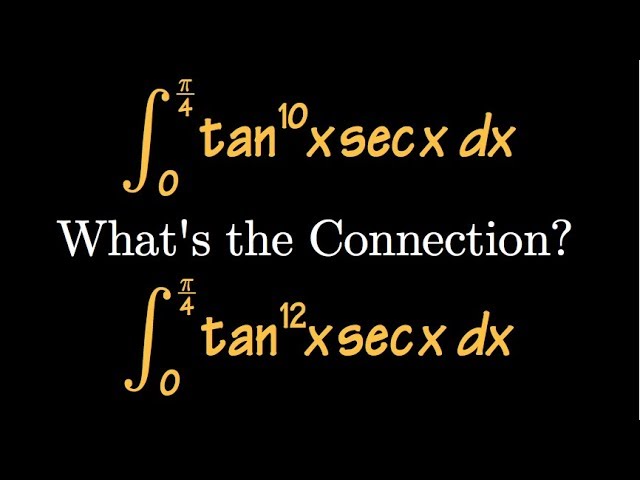
Показать описание
Integration by Parts challenge problem, integral of tan^12(x)*sec(x) from 0 to pi/4, Connecting these Two Integrals with Integration by Parts
Please subscribe for more math content!
Check out my site & social media
Thank you for your support!
blackpenredpen | 曹老師
Please subscribe for more math content!
Check out my site & social media
Thank you for your support!
blackpenredpen | 曹老師
Connecting these Two Integrals with Integration by Parts
How to do two (or more) integrals with just one
Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
Finding the Area Between Two Curves by Integration
What is Integration? 3 Ways to Interpret Integrals
Proof that derivatives and integrals are inverse operators geometrically
Indefinite Integrals (1 of 2: Making Connections with areas and volumes through integrals)
What is Jacobian? | The right way of thinking derivatives and integrals
Can we do a direct substitution between these two integrals?
What does area have to do with slope? | Chapter 9, Essence of calculus
Recurrence Relation - worked example (2 of 2: Connecting the integrals)
Integration (Calculus)
Indefinite Integrals (2 of 2: Finding the connection between Volumes, Areas and Corner Lengths)
Fundamental Theorem of Calculus Part 1
Fundamental theorem of calculus (Part 2) | AP Calculus AB | Khan Academy
Calculus 3 Lecture 14.2: How to Solve Double/Repeated/Iterated Integrals
Intro to Further Integration (1 of 2: Expanding on prior learning)
Evaluate the integral by reversing the order of integration
Calculus - Lesson 15 | Relation between Differentiation and Integration | Don't Memorise
What is Integration? Finding the Area Under a Curve
Calculus 3 Lecture 14.1: INTRODUCTION to Double Integrals (Background Info)
Calculus 3: Line Integrals (18 of 44) What is a Line Integral? [(y)dx+(z)dy+(x)dz] Example 6
What is Application Integration?
Example of the Fundamental Theorem of Line Integrals
Комментарии
 0:10:08
0:10:08
 0:18:03
0:18:03
 0:20:46
0:20:46
 0:07:52
0:07:52
 0:10:55
0:10:55
 0:08:16
0:08:16
 0:08:23
0:08:23
 0:27:14
0:27:14
 0:09:18
0:09:18
 0:12:39
0:12:39
 0:07:57
0:07:57
 0:07:04
0:07:04
 0:10:25
0:10:25
 0:11:30
0:11:30
 0:04:45
0:04:45
 3:23:48
3:23:48
 0:16:49
0:16:49
 0:08:15
0:08:15
 0:08:40
0:08:40
 0:08:18
0:08:18
 0:51:58
0:51:58
 0:05:03
0:05:03
 0:10:28
0:10:28
 0:14:21
0:14:21