filmov
tv
A Diophantine Equation (x^2-xy+y^2=x+y)

Показать описание
This video is about a number theory problem
Send me a tweet at @SyberMath if you want to share a picture of your solution/ideas and comment here with the link to the tweet.
#NumberTheoryProblems #DiophantineEquations
EXPLORE:
Send me a tweet at @SyberMath if you want to share a picture of your solution/ideas and comment here with the link to the tweet.
#NumberTheoryProblems #DiophantineEquations
EXPLORE:
A Diophantine Equation (x^2-xy+y^2=x+y)
A Diophantine Equation x^2 xy+y^2=x+y
Solving x^2+xy+y^2=x^2y^2
A Diophantine Equation 2xy + x + y = 9 #numbersystem #mathskills #algebricexpression#viralmaths
Integral Solutions of the Binary Quadratic Diophantine Equation x2 - 2xy -y2 + 2x +14y= 72
Can You Solve this Trending Problem with Ease? | x +2xy + y =22 | Find Positive Integer Solutions
X^2+Y^2=13, X-Y=5, X=?,Y=? | ALGEBRAIC EQUATIONS MATHS OLYMPIAD | ALGEBRAIC PROBLEMS | ALGEBRA MATHS
5 simple unsolvable equations
A Quadratic Diophantine Equation | Math Olympiads
When mathematicians get bored (ep1)
An Algebra Problem | x^2+y^2+z^2=xy+xz+yz
Cool Trick for Solving the Diophantine Equation (x+y)^2=x^3+y^3 | Integer Solution | Math Olympiad
Solving a Diophantine Equation 𝑥^2+𝑦^2=(𝑥𝑦−7)^2
Solving x+y=(x-y)^2, a Diophantine Equation
A Diophantine Equation | Integer Solutions
A Hyperbolic Diophantine Equation
A Nice Diophantine Equation in Number Theory | You Should Learn This Theorem | Math Olympiad
Solving the differential equation xy'+2y=x^3
A nice Diophantine equation||x+xy+y=64 #olympiad #trending
Diophantine Equation | x+xy+y=54
A Wonderful Math Olympiad Question. Nice Algebra Problem. x^2 -y^2=24, xy=35 ,x+y=?
Diophantine Equations: Strategies and Examples
।। if, x²-y²=24 and xy=35 then, x+y=? ।। A nice algebraic problem @mathscuriosity494
Solve the simultaneous equations, x^2+y^2=100, x+y+xy=34. Using a simpler approach
Комментарии
 0:15:44
0:15:44
 0:15:44
0:15:44
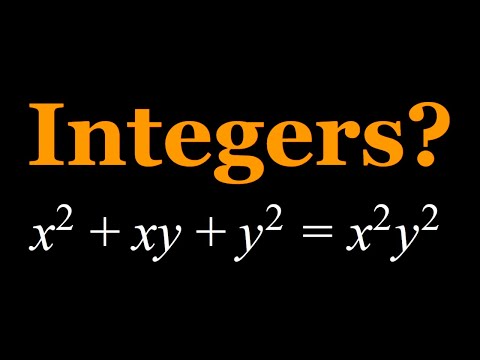 0:07:34
0:07:34
 0:05:02
0:05:02
 0:01:47
0:01:47
 0:08:01
0:08:01
 0:09:22
0:09:22
 0:00:50
0:00:50
 0:10:19
0:10:19
 0:00:37
0:00:37
 0:00:53
0:00:53
 0:03:51
0:03:51
 0:04:11
0:04:11
 0:10:57
0:10:57
 0:10:00
0:10:00
 0:04:52
0:04:52
 0:07:40
0:07:40
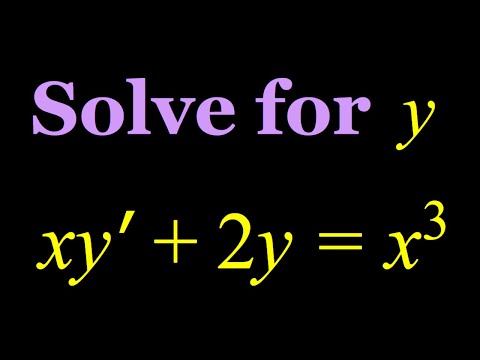 0:08:16
0:08:16
 0:06:38
0:06:38
 0:05:12
0:05:12
 0:07:25
0:07:25
 0:27:34
0:27:34
 0:13:38
0:13:38
 0:06:23
0:06:23